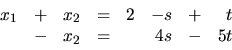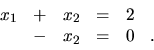Uvažujme konečne o všeobecnej sústave 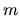 lineárnych rovníc s
lineárnych rovníc s 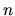 neznámymi
neznámymi
zapísanej pre vhodne definovanú maticu A, vektory x,b aj v
tvare 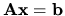 .
Vieme, že nutná a postačujúca podmienka pre to, aby sústava
(4.7) mala riešenie, je
.
Vieme, že nutná a postačujúca podmienka pre to, aby sústava
(4.7) mala riešenie, je
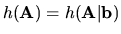 . Nech
sústava (4.7) má riešenie. Ak
. Nech
sústava (4.7) má riešenie. Ak 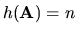 , tak
(4.7) má jediné riešenie. Ak
, tak
(4.7) má jediné riešenie. Ak 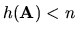 , tak
(4.7) má nekonečne veľa riešení. Tieto tvrdenia spolu s postupom
použitým pri GEM (a pri zisťovaní hodnosti matice) a spôsobom
riešenia homogénnej sústavy rovníc využívame pri riešení
(4.7).
, tak
(4.7) má nekonečne veľa riešení. Tieto tvrdenia spolu s postupom
použitým pri GEM (a pri zisťovaní hodnosti matice) a spôsobom
riešenia homogénnej sústavy rovníc využívame pri riešení
(4.7).
 Prípad
Prípad
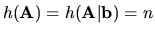 .
.
Príklad 15.
Zistite, či sústava rovníc
má riešenie a ak áno, určte ho.
Riešenie:
Známym spôsobom dospejeme ku ekvivalentnej sústave
Vidno, že
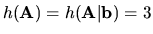 , a preto existuje jediné
riešenie tejto sústavy. Spätná substitúcia len potvrdzuje toto
tvrdenie. Preto
, a preto existuje jediné
riešenie tejto sústavy. Spätná substitúcia len potvrdzuje toto
tvrdenie. Preto 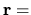
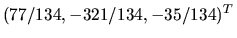 .
.

 Prípad
Prípad
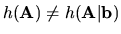 .
.
Príklad 16.
Zistite, či sústava rovníc
má riešenie a ak áno, určte ho.
Riešenie:
Ihneď dostávame
Potom
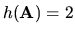 ,
,
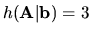 , a preto sústava nemá
riešenie. Nemuseli sme použiť Frobeniusovu vetu. Z ekvivalentnej
sústavy vidno, že je sporná. Nemôže súčasne platiť
, a preto sústava nemá
riešenie. Nemuseli sme použiť Frobeniusovu vetu. Z ekvivalentnej
sústavy vidno, že je sporná. Nemôže súčasne platiť 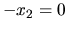 a
a
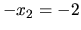 .
.

 Prípad
Prípad
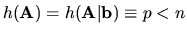 .
.
V tomto prípade má sústava 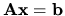 nekonečne veľa
riešení. Všetky riešenia sú tvaru
nekonečne veľa
riešení. Všetky riešenia sú tvaru
kde
- *
- w je nejaké riešenie sústavy Ax=b
- *
-
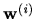 sú lineárne nezávislé riešenia odpovedajúcej homogénnej sústavy
rovníc Ax=0 , pre
sú lineárne nezávislé riešenia odpovedajúcej homogénnej sústavy
rovníc Ax=0 , pre
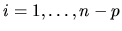
- *
-
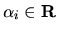 pre
pre
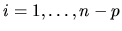 .
.
Často sa hovorí, že riešenie r je v tvare súčtu
partikulárneho (nejakého) riešenia sústavy Ax=b a
všeobecného riešenia odpovedajúcej homogénnej sústavy Ax=0. Pri
troche zručnosti sa tieto dve úlohy dajú riešiť spoločne.
Príklad 17.
Zistite, či sústava lineárnych rovníc
má riešenie a ak áno, určte ho.
Riešenie:
Známym spôsobom dospejeme ku ekvivalentnej sústave
Vidno, že
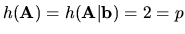 . Teda sústava má
nekonečne veľa riešení.
. Teda sústava má
nekonečne veľa riešení.
V časti o homogénnych sústavach sme zistili, že dve lineárne
nezávislé riešenia odpovedajúcej homogénnej sústavy lineárnych
rovníc sú
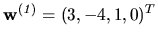 a
a
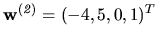 . Za parametre sme pritom zvolili
neznáme
. Za parametre sme pritom zvolili
neznáme 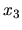 a
a 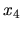 .
.
Nejaké (partikulárne) riešenie Ax=b dostaneme z ekvivalentnej
sústavy
najjednoduchšie tak, že v nej zvolíme za parametre 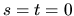 . Dostávame sústavu
. Dostávame sústavu
Potom už
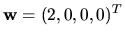 . Teda všeobecné riešenie sústavy
rovníc je tvaru
. Teda všeobecné riešenie sústavy
rovníc je tvaru
kde
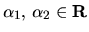 . Všimnite si, že za
partikulárne riešenie sústavy Ax=b sme mohli zvoliť aj vektor
. Všimnite si, že za
partikulárne riešenie sústavy Ax=b sme mohli zvoliť aj vektor
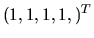 . Potom by bolo všeobecné riešenie tvaru
. Potom by bolo všeobecné riešenie tvaru
Dosadením sa dá zistiť, že 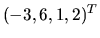 je tiež riešením
sústavy. Môžeme ho vyjadriť ako
je tiež riešením
sústavy. Môžeme ho vyjadriť ako
ale aj

Subsections
![]() Prípad
Prípad
![]() .
.
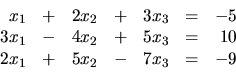
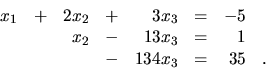
![]()
![]() Prípad
Prípad
![]() .
.
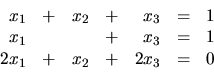
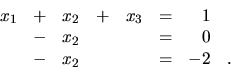
![]() Prípad
Prípad
![]() .
.
![]() nekonečne veľa
riešení. Všetky riešenia sú tvaru
nekonečne veľa
riešení. Všetky riešenia sú tvaru
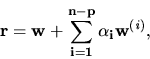
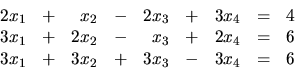
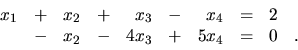
![]() a
a
![]() . Za parametre sme pritom zvolili
neznáme
. Za parametre sme pritom zvolili
neznáme ![]() a
a ![]() .
.