Číselnou množinou nazývame takú množinu, ktorej všetky
prvky sú čísla.
Majme číselnú množinu 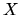 . Nech
. Nech 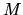 je také číslo
z
je také číslo
z 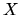 , že
pre všetky
, že
pre všetky 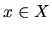 platí
platí 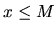 . Číslo
. Číslo 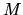 nazývame
maximum množiny
nazývame
maximum množiny 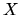 a označujeme ho
a označujeme ho 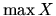 .
.
Nech 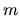 je také číslo z množiny
je také číslo z množiny 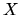 , že
pre všetky
, že
pre všetky 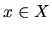 platí
platí 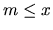 .
Číslo
.
Číslo 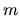 nazývame
minimum množiny
nazývame
minimum množiny 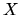 a označujeme ho
a označujeme ho 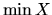 .
.
Každá konečná číselná množina má maximum a minimum.
Číselná množina 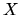 sa nazýva zhora ohraničená, ak
existuje také číslo
sa nazýva zhora ohraničená, ak
existuje také číslo 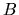 , že pre každé číslo
, že pre každé číslo 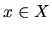 platí
platí 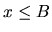 . Číselná množina
. Číselná množina 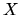 sa nazýva
zdola ohraničená, ak
existuje také číslo
sa nazýva
zdola ohraničená, ak
existuje také číslo 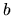 , že pre každé číslo
, že pre každé číslo 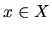 platí
platí 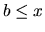 . Číslo
. Číslo 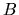 nazývame horným ohraničením množiny
nazývame horným ohraničením množiny 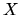 a číslo
a číslo 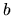 nazývame dolným
ohraničením množiny
nazývame dolným
ohraničením množiny 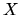 . Množina ohraničená zdola aj zhora
sa nazýva ohraničená. Najmenšie horné ohraničenie množiny
. Množina ohraničená zdola aj zhora
sa nazýva ohraničená. Najmenšie horné ohraničenie množiny 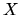 sa nazýva supremum množiny
sa nazýva supremum množiny 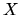 a označujeme ho
a označujeme ho 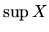 . Najväčšie dolné ohraničenie množiny
. Najväčšie dolné ohraničenie množiny 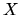 sa nazýva infimum množiny
sa nazýva infimum množiny 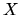 a označujeme ho
a označujeme ho 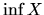 . Majú tieto vlastnosti:
. Majú tieto vlastnosti:
- Pre každé
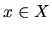 platí
platí
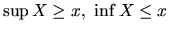
- Pre každé
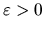 existujú čísla
existujú čísla
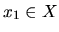 a
a 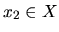 , pre ktoré platí
, pre ktoré platí
- Ak množina
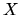 je ohraničená zhora, tak má supremum.
Ak množina
je ohraničená zhora, tak má supremum.
Ak množina 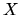 je ohraničená zdola, tak má infimum.
je ohraničená zdola, tak má infimum.
- Ak
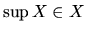 , tak
, tak
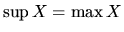 .
Ak
.
Ak 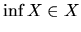 , tak
, tak
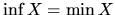 .
.
Nech 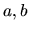 sú reálne čísla a nech
sú reálne čísla a nech 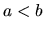 . Množinu čísel
. Množinu čísel 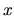 , pre ktoré platí :
, pre ktoré platí :
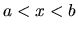 nazývame otvoreným intervalom
a označujeme ho
nazývame otvoreným intervalom
a označujeme ho 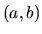 .
Pre takýto interval platí:
.
Pre takýto interval platí:
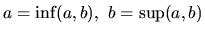 . Minimum a maximum neexistuje.
. Minimum a maximum neexistuje.
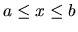 nazývame uzavretým intervalom
a označujeme ho
nazývame uzavretým intervalom
a označujeme ho
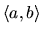 .
Platí:
.
Platí:
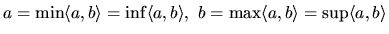 .
.
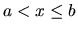 nazývame zľava otvoreným a sprava
uzavretým intervalom
a označujeme ho
nazývame zľava otvoreným a sprava
uzavretým intervalom
a označujeme ho 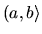 .
Platí:
.
Platí:
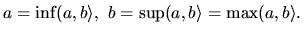 Minimum neexistuje.
Minimum neexistuje.
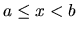 nazývame zľava uzavretým a sprava
otvoreným intervalom
a označujeme ho
nazývame zľava uzavretým a sprava
otvoreným intervalom
a označujeme ho 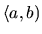 .
Platí:
.
Platí:
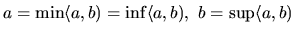 . Maximum neexistuje.
. Maximum neexistuje.
Intervalmi nazývame aj množiny všetkých čísel 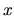 určených nerovnosťami:
určených nerovnosťami:
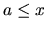 , označujeme
, označujeme
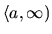 - zľava uzavretý
interval od
- zľava uzavretý
interval od
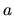 do nekonečna.
Platí:
do nekonečna.
Platí:
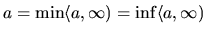 . Maximum a supremum neexistuje.
. Maximum a supremum neexistuje.
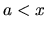 , označujeme
, označujeme 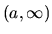 - zľava otvorený interval od
- zľava otvorený interval od
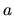 do nekonečna.
Platí:
do nekonečna.
Platí:
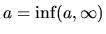 . Minimum, maximum a supremum neexistujú.
. Minimum, maximum a supremum neexistujú.
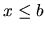 , označujeme
, označujeme
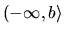 - sprava uzavretý interval od
mínus nekonečna po
- sprava uzavretý interval od
mínus nekonečna po 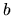 .
Platí:
.
Platí:
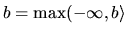
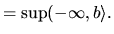 Minimum a infimum neexistujú.
Minimum a infimum neexistujú.
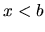 , označujeme
, označujeme 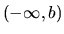 - sprava otvorený interval od
mínus nekonečna po
- sprava otvorený interval od
mínus nekonečna po 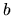 .
Platí:
.
Platí:
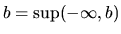 . Maximum, minimum a infimum neexistujú.
. Maximum, minimum a infimum neexistujú.
Množinu všetkých reálnych čísel môžeme označovať aj
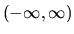 .
.
Okolím čísla 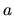 (bodu
(bodu 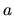 ) nazývame otvorený
interval, ktorý číslo
) nazývame otvorený
interval, ktorý číslo 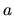 obsahuje. Označujeme ho
obsahuje. Označujeme ho 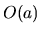 .
.
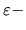 okolie bodu
okolie bodu 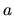 je interval
je interval
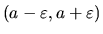 ,
pričom
,
pričom
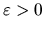 .
.
Pre riešenie nasledujúcich príkladov, kde budeme dokazovať,
že nejaké číslo je infimom alebo supremom množiny,
nám bude užitočná nasledujúca veta:
Veta 1.2
Archimedova vlastnosť: Pre ľubovoľné reálne číslo 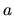 existuje také prirodzené číslo
existuje také prirodzené číslo 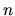 , že platí:
, že platí: 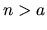 .
.
Príklad 1.
Nájdime supremum, infimum, maximum a minimum množiny
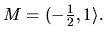
Riešenie:
Zo znázornenia danej množiny na číselnej osi usúdime, že
supremum množiny je číslo 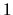 a infimum množiny
a infimum množiny 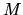 je číslo
je číslo 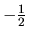 . Ukážeme, že je to tak. Čísla
. Ukážeme, že je to tak. Čísla 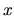 , ktoré
tvoria množinu
, ktoré
tvoria množinu 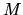 , spĺňajú nerovnicu
, spĺňajú nerovnicu
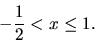 |
(1.1) |
Z toho vyplýva, že daná množina je ohraničená a číslo
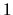 je jedno z horných ohraničení, číslo
je jedno z horných ohraničení, číslo 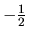 je
jedno z dolných ohraničení. Ukážeme, že číslo
je
jedno z dolných ohraničení. Ukážeme, že číslo 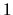 je najmenším horným ohraničením, t.j.
je najmenším horným ohraničením, t.j. 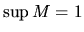 .
Musí preto spĺňať vlastnosti suprema:
.
Musí preto spĺňať vlastnosti suprema:
1. 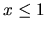 pre každé
pre každé 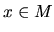 .
.
2. Ku každému
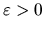 existuje
také číslo
existuje
také číslo 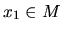 , pre ktoré platí
, pre ktoré platí
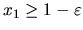 .
Prvé tvrdenie vyplýva z nerovnosti (1.1). Druhé tvrdenie dokážeme tak, že ak za
.
Prvé tvrdenie vyplýva z nerovnosti (1.1). Druhé tvrdenie dokážeme tak, že ak za 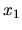 vezmeme číslo
vezmeme číslo 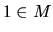 ,
potom pre každé
,
potom pre každé 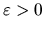 platí
platí
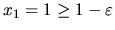 .
.
Podobne dokazujeme, že
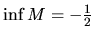 :
:
1.
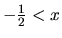 , pre všetky
, pre všetky 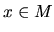 - vyplýva z nerovnosti
(1.1).
- vyplýva z nerovnosti
(1.1).
2. Ak zvolíme
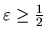 , potom číslo
, potom číslo 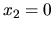 , tak platí
, tak platí
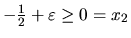 . Ak zvolíme
. Ak zvolíme
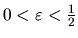 , potom číslo
, potom číslo
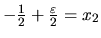 je prvkom množiny
je prvkom množiny 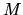 , pre ktorý platí
, pre ktorý platí
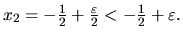 Z toho vyplýva že
Z toho vyplýva že
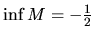 .
Číslo
.
Číslo 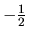 nie je z množiny
nie je z množiny 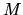 , preto podľa vlastnosti
, preto podľa vlastnosti
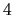 pre infimum množina
pre infimum množina 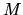 nemá minimum. Číslo
nemá minimum. Číslo 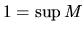 je z množiny
je z množiny 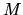 a preto podľa vlastnosti
a preto podľa vlastnosti 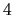 je číslo
je číslo 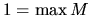 .
. 
Príklad 2.
Nájdime supremum, infimum, maximum a minimum množiny 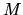 , kde
, kde 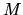 je
množina všetkých čísel tvaru
je
množina všetkých čísel tvaru
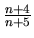 , kde
, kde 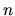 je
prirodzené číslo.
je
prirodzené číslo.
Riešenie:
Vypočítame
niekoľko prvkov
tejto množiny:
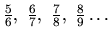 Z toho usudzujeme, že
Z toho usudzujeme, že 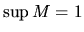 a
a
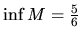 . Dokážeme to.
. Dokážeme to.
Vlastnosť číslo 1 je skutočne splnená:
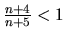
Ukážeme druhú vlastnosť:
Zvolíme
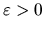 . Treba nájsť prvok
. Treba nájsť prvok 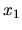 z množiny
z množiny 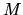 tak, aby platilo:
tak, aby platilo:
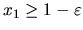 .
.
Keďže 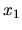 je prvok z
je prvok z 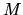 , musí byť tvaru
, musí byť tvaru
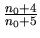 pre
nejaké
pre
nejaké
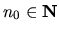 . Potom musí platiť:
. Potom musí platiť:
z čoho po úprave dostávame
Z Archimedovej vlastnosti ale takéto 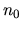 vždy existuje pre ľubovoľné
vždy existuje pre ľubovoľné 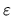 . Tým je dokázaná aj druhá vlastnosť
suprema, a preto
. Tým je dokázaná aj druhá vlastnosť
suprema, a preto 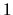 je naozaj supremom množiny
je naozaj supremom množiny 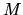 .
.
Podobne dokážeme, že
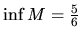 .
Prvá vlastnosť: Z nerovnosti
.
Prvá vlastnosť: Z nerovnosti 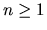 vyplýva
vyplýva
Druhá vlastnosť: Pre každé 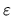 treba nájsť prvok
treba nájsť prvok
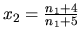 , pre ktorý bude platiť:
, pre ktorý bude platiť:
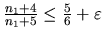 . Stačí ale zvoliť
. Stačí ale zvoliť 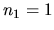 a potom
nerovnosť
a potom
nerovnosť
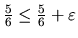 platí pre ľubovoľné
platí pre ľubovoľné
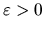 . Preto
. Preto
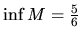 .
.
Supremum množiny 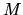 nepatrí do
nepatrí do 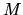 , preto množina nemá maximum.
Infimum množiny
, preto množina nemá maximum.
Infimum množiny 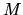 je prvkom tejto množiny, a preto
je prvkom tejto množiny, a preto
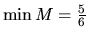 .
. 
Subsections
![]() . Nech
. Nech ![]() je také číslo
z
je také číslo
z ![]() , že
pre všetky
, že
pre všetky ![]() platí
platí ![]() . Číslo
. Číslo ![]() nazývame
maximum množiny
nazývame
maximum množiny ![]() a označujeme ho
a označujeme ho ![]() .
.
![]() je také číslo z množiny
je také číslo z množiny ![]() , že
pre všetky
, že
pre všetky ![]() platí
platí ![]() .
Číslo
.
Číslo ![]() nazývame
minimum množiny
nazývame
minimum množiny ![]() a označujeme ho
a označujeme ho ![]() .
.
![]() sa nazýva zhora ohraničená, ak
existuje také číslo
sa nazýva zhora ohraničená, ak
existuje také číslo ![]() , že pre každé číslo
, že pre každé číslo ![]() platí
platí ![]() . Číselná množina
. Číselná množina ![]() sa nazýva
zdola ohraničená, ak
existuje také číslo
sa nazýva
zdola ohraničená, ak
existuje také číslo ![]() , že pre každé číslo
, že pre každé číslo ![]() platí
platí ![]() . Číslo
. Číslo ![]() nazývame horným ohraničením množiny
nazývame horným ohraničením množiny ![]() a číslo
a číslo ![]() nazývame dolným
ohraničením množiny
nazývame dolným
ohraničením množiny ![]() . Množina ohraničená zdola aj zhora
sa nazýva ohraničená. Najmenšie horné ohraničenie množiny
. Množina ohraničená zdola aj zhora
sa nazýva ohraničená. Najmenšie horné ohraničenie množiny ![]() sa nazýva supremum množiny
sa nazýva supremum množiny ![]() a označujeme ho
a označujeme ho ![]() . Najväčšie dolné ohraničenie množiny
. Najväčšie dolné ohraničenie množiny ![]() sa nazýva infimum množiny
sa nazýva infimum množiny ![]() a označujeme ho
a označujeme ho ![]() . Majú tieto vlastnosti:
. Majú tieto vlastnosti:
![]()
![]() a infimum množiny
a infimum množiny ![]() je číslo
je číslo ![]() . Ukážeme, že je to tak. Čísla
. Ukážeme, že je to tak. Čísla ![]() , ktoré
tvoria množinu
, ktoré
tvoria množinu ![]() , spĺňajú nerovnicu
, spĺňajú nerovnicu
![]() , kde
, kde ![]() je
množina všetkých čísel tvaru
je
množina všetkých čísel tvaru
![]() , kde
, kde ![]() je
prirodzené číslo.
je
prirodzené číslo.
![]() Z toho usudzujeme, že
Z toho usudzujeme, že ![]() a
a
![]() . Dokážeme to.
. Dokážeme to.
![]()
![]() . Treba nájsť prvok
. Treba nájsť prvok ![]() z množiny
z množiny ![]() tak, aby platilo:
tak, aby platilo:
![]() .
.
![]() je prvok z
je prvok z ![]() , musí byť tvaru
, musí byť tvaru
![]() pre
nejaké
pre
nejaké
![]() . Potom musí platiť:
. Potom musí platiť: