Množinu C všetkých usporiadaných dvojíc
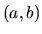 , kde
, kde
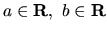 nazývame množinou
komplexných čísel, ak pre každé
dva prvky
nazývame množinou
komplexných čísel, ak pre každé
dva prvky 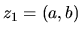 ,
, 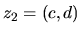 z množiny C je definovaná
rovnosť, sčítanie a násobenie takto:
z množiny C je definovaná
rovnosť, sčítanie a násobenie takto:
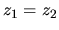 práve vtedy, keď
práve vtedy, keď 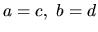 ,
,
-
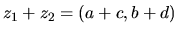 ,
,
-
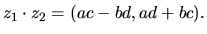
Pre sčítanie a násobenie kompexných čísel platí
asociatívny a komutatívny zákon. Násobenie
komplexných čísel
je distributívne vzhľadom na sčítanie komplexných
čísel.
Nech 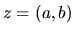 je komplexné číslo. Potom číslo
je komplexné číslo. Potom číslo 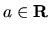 nazývame reálnou časťou a číslo
nazývame reálnou časťou a číslo 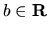 imaginárnou časťou komplexného čísla
imaginárnou časťou komplexného čísla 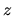 .
Označujeme ich takto:
.
Označujeme ich takto:
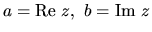 .
.
Komplexné číslo 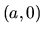 stotožňujeme s
reálnym číslom
stotožňujeme s
reálnym číslom 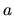 :
: 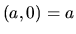 . Komplexné číslo
. Komplexné číslo
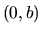 , kde
, kde 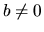 , nazývame rýdzoimaginárnym
číslom. Číslo
, nazývame rýdzoimaginárnym
číslom. Číslo 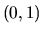 nazývame
imaginárnou jednotkou a označujeme ho
nazývame
imaginárnou jednotkou a označujeme ho
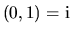 .
Komplexné číslo
.
Komplexné číslo 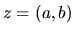 píšeme aj v tvare:
píšeme aj v tvare:
Komplexné číslo 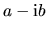 nazývame komplexne
združeným ku komplexnému číslu
nazývame komplexne
združeným ku komplexnému číslu 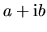 .
Absolútnou hodnotou alebo modulom
komplexného čísla
.
Absolútnou hodnotou alebo modulom
komplexného čísla 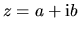 nazývame číslo
nazývame číslo
Ak pre komplexné číslo 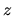 platí:
platí: 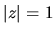 , nazývame ho
komplexnou jednotkou. Každú komplexnú jednotku
, nazývame ho
komplexnou jednotkou. Každú komplexnú jednotku 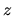 možno
písať v tvare:
možno
písať v tvare:
kde 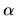 je reálne číslo. Toto číslo označujeme aj
je reálne číslo. Toto číslo označujeme aj
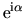 a platí:
a platí:
Argumentom komplexného čísla
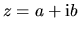 , kde
, kde 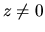 ,
nazývame číslo
,
nazývame číslo
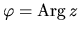 , pre ktoré platí:
, pre ktoré platí:
Ak 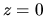 , tak Arg
, tak Arg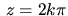 , kde
, kde 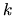 je celé číslo.
Ak pre číslo
je celé číslo.
Ak pre číslo 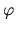 platí:
platí:
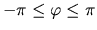 , nazývame ho
hlavnou hodnotou argumentu a ozančujeme ho arg
, nazývame ho
hlavnou hodnotou argumentu a ozančujeme ho arg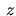 .
.
Každé komplexné číslo 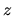 možno vyjadriť v goniometrickom tvare:
možno vyjadriť v goniometrickom tvare:
kde
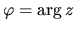 , alebo v exponenciálnom tvare:
, alebo v exponenciálnom tvare:
kde
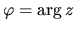 .
.
Veta 1.1
Pre číslo i platí: