Pri aplikáciách matematiky je často potrebné pracovať s hodnotami
komplikovaných funkcií. Je možné nahradiť ich hodnotami
jednoduchších funkcií, ak sú tieto v rámci požadovanej presnosti.
Často sa k tomu používajú lineárne funkcie, keďže sú na výpočty
najjednoduchšie.
Nech má funkcia 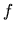 v bode
v bode 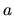 deriváciu. Potom hodnoty funkcie
deriváciu. Potom hodnoty funkcie 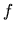 v blízkom okolí čísla
v blízkom okolí čísla 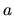 najlepšie zo všetkých lineárnych funkcií
aproximuje (približne vyjadruje) funkcia
najlepšie zo všetkých lineárnych funkcií
aproximuje (približne vyjadruje) funkcia
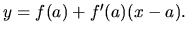 Preto
Preto
pre čísla 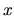 blízke číslu
blízke číslu 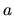 .
Lineárny výraz
.
Lineárny výraz
v tejto aproximácii voláme diferenciál funkcie 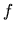 v bode
v bode 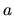 .
Všeobecne diferenciál n-tého rádu funkcie
.
Všeobecne diferenciál n-tého rádu funkcie 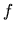 v bode
v bode 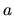 je výraz
je výraz
ak existuje 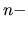 tá derivácia funkcie
tá derivácia funkcie 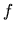 v bode
v bode 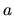 .
.
Špeciálne, pre 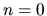 , diferenciálom nultého rádu je konštantna
, diferenciálom nultého rádu je konštantna
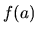 .
.
Príklad 22.
Nájdeme prvých päť diferenciálov funkcie
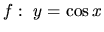 v bode
v bode 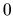 .
.
Riešenie: K nájdeniu diferenciálu potrebujeme príslušnú deriváciu v danom
bode. Keďže
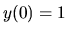 ,
, 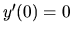 ,
, 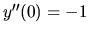 ,
, 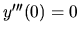 ,
,
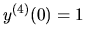 ,
,
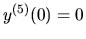 , platí
, platí
Ostatné hľadané diferenciály sú rovné nulovej konštante.

Pre použitie pojmu diferenciálu pozri časť 7.8.
![]() v bode
v bode ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() , platí
, platí