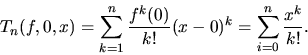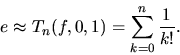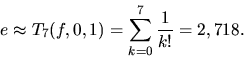Približné výpočty hodnôt funkcií
Ak máme približne vypočítať hodnotu funkcie 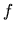 v bode
v bode 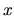 , ktorú nie sme
z nejakého dôvodu schopní vypočítať presne, postupujeme nasledovne.
, ktorú nie sme
z nejakého dôvodu schopní vypočítať presne, postupujeme nasledovne.
- Nájdeme taký bod
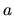 čo najbližšie k bodu
čo najbližšie k bodu 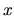 , v ktorom
sme schopní vypočítať hodnotu funkcie
, v ktorom
sme schopní vypočítať hodnotu funkcie 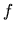 a jej derivácií.
a jej derivácií.
- Použijeme vzťah
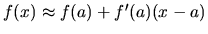 .
.
- Ak nie sme spokojní s presnosťou aproximácie, použijeme vzťah
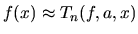 pre vhodné prirodzené číslo
pre vhodné prirodzené číslo 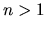 .
.
Príklad 25.
Vypočítajme pomocou prvého diferenciálu približne hodnotu
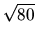 .
.
Riešenie: Ide o výpočet hodnoty 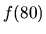 pre funkciu
pre funkciu
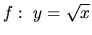 .
Keďže
.
Keďže
potrebujeme nájsť vhodnú hodnotu 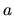 blízko hodnoty
blízko hodnoty 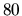 , v ktorej
vieme vypočítať obidve hodnoty
, v ktorej
vieme vypočítať obidve hodnoty 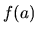 aj
aj 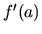 . Keďže
. Keďže
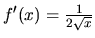 , vhodnou hodnotou je
, vhodnou hodnotou je 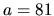 . Platí
. Platí
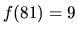 a
a
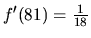 . Preto
. Preto

Príklad 26.
Vypočítajme s presnosťou na tri desatinné miesta hodnotu
čísla 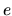 .
.
Riešenie: Použijeme Taylorov mnohočlen funkcie 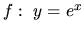 v bode
v bode 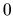 .
Platí
.
Platí
Keďže 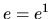 , je
, je
Potrebnú hodnotu 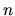 určíme z požiadavky, aby chyba výpočtu bola
menšia ako
určíme z požiadavky, aby chyba výpočtu bola
menšia ako
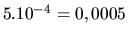 (tri desatinné miesta!). Z Taylorovej
vety vyplýva, že chyba výpočtu sa rovná hodnote
(tri desatinné miesta!). Z Taylorovej
vety vyplýva, že chyba výpočtu sa rovná hodnote
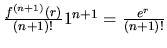 ,
kde
,
kde 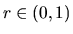 . Preto číslo
. Preto číslo 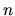 , pre ktoré bude výpočet
zaručene v rámci danej presnosti je určené nerovnicou
, pre ktoré bude výpočet
zaručene v rámci danej presnosti je určené nerovnicou
teda
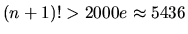 . Najmenšie prirodzené číslo
. Najmenšie prirodzené číslo 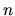 ,
ktoré spĺňa túto nerovnosť, nájdeme pomocou výpočtu faktoriálov:
,
ktoré spĺňa túto nerovnosť, nájdeme pomocou výpočtu faktoriálov:
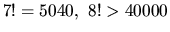 . Z toho vyplýva, že
. Z toho vyplýva, že 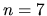 .
Preto
.
Preto
Porovnajte túto hodnotu výpočtom kalkulačkou! Poznamenajme, že
rovnakú hodnotu dostaneme aj voľbou 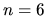 .
.

![]() .
.
![]() pre funkciu
pre funkciu
![]() .
Keďže
.
Keďže
![]() .
.
![]() v bode
v bode ![]() .
Platí
.
Platí