Spojitosť a riešenie rovníc

Ak $f$ je spojitá funkcia v intervale $\langle a,b\rangle$ a $f(a)$ a $f(b)$ majú opačné znamienka, tak rovnica $f(x)=0$ má v intervale $(a,b)$ aspoň jedno riešenie.

Pre použitie tejto vlastnosti pozri časť 6.6 a 7.14.

Príklad 17. Zistime body nespojitosti funkcií $e(x)=4x^3-5x$, $f(x)=\frac{x+1}{x-1}$, $g(x)=\{x\}.[x+1]$, $h(x)=sign(8+2x-x^2)$.

Riešenie: Funkcie $e$ a $f$ sú elementárne a preto spojité. Prvá funkcia je aj spojitá v ${\bf R}$, druhá má bod nespojitosti v čísle $1$. Obidve funkcie $\{x\}$ aj $[x]$ sú spojité v každej neceločíselnej hodnote $x$ a preto aj ich súčin, funkcia $g$ je spojitá v týchto číslach. Ak načrtneme graf $g$, vidíme, že je nespojitá vo všetkých celých číslach s výnimkou čísla $1$. Funkcia $h$ bude nespojitá v tých číslach, v ktorých sa mení znamienko funkcie $y = 8+2x-x^2$ (odôvodnite!) a to sú čísla $-2$ a $4$. $\clubsuit$

Príklad 18. Nájdime číslo $p$, pre ktoré je funkcia $f$ definovaná po častiach

$$f(x) = \left\{ \begin{array}{ll} 3x-p, & x \leq 0 \\ x^2+2, & x > 0 \end{array} \right.$$

spojitá.

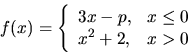
Riešenie: Keďže obidve funkcie $y = 3x-p$ aj $y = x^2+2$ sú spojité (tá prvá pre každú hodnotu $p$), funkcia $f$ je nezávisle na hodnote $p$ spojitá v každom nenulovom čísle. Ak načrtneme graf funkcie $f$ v intervale $(0,\infty)$, vidíme, že pre hodnoty $x$ "blízke" $0$ sú hodnoty $f(x)$ "blízke" $2$. Aby bola funkcia $f$ spojitá v čísle $0$, je nutné (a postačujúce), aby $f(0) = 3.0-p = 2$, preto $p = -2$. $\clubsuit$