Matematická formulácia tohoto problému je nasledovná:
Je daná spojitá funkcia
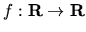 , definovaná na intervale
, definovaná na intervale
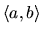 .
Chceme nájsť reálne číslo
.
Chceme nájsť reálne číslo
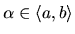 (pokiaľ existuje),
pre ktoré platí
(pokiaľ existuje),
pre ktoré platí
Takéto číslo 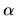 nazývame koreň rovnice.
Keďže funkcia
nazývame koreň rovnice.
Keďže funkcia 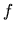 môže byť v podstate ľubovoľná
funkcia jednej reálnej premennej, jej koreň vo všeobecnosti nevieme nájsť
nejakým matematickým výpočtom ako napríklad u lineárnej
alebo kvadratickej funkcie,
prípadne niektorej goniometrickej funkcie. Tento koreň preto budeme
hľadať numerickými metódami. Spravidla sa nám nepodarí nájsť
koreň, ale len jeho aproximáciu - približnú hodnotu.
Musí nás preto zaujímať okrem metódy,
ktorú na výpočet použijeme, aj chyba,
akej sa pri nájdení tohoto približného riešenia dopustíme
(podrobnejšie o numerických metódach a chybách
pozri kapitolu Reálne
čísla, paragrafy Zdroje chýb, Chyby aritmetických operácií ).
Numerické metódy, ktorými sa budeme teraz zaoberať,
sú založené na
iteračných princípoch (pozri kapitolu Reálne čísla,
paragraf
Algoritmy).
Budú nás zaujímať hlavne dve základné otázky:
môže byť v podstate ľubovoľná
funkcia jednej reálnej premennej, jej koreň vo všeobecnosti nevieme nájsť
nejakým matematickým výpočtom ako napríklad u lineárnej
alebo kvadratickej funkcie,
prípadne niektorej goniometrickej funkcie. Tento koreň preto budeme
hľadať numerickými metódami. Spravidla sa nám nepodarí nájsť
koreň, ale len jeho aproximáciu - približnú hodnotu.
Musí nás preto zaujímať okrem metódy,
ktorú na výpočet použijeme, aj chyba,
akej sa pri nájdení tohoto približného riešenia dopustíme
(podrobnejšie o numerických metódach a chybách
pozri kapitolu Reálne
čísla, paragrafy Zdroje chýb, Chyby aritmetických operácií ).
Numerické metódy, ktorými sa budeme teraz zaoberať,
sú založené na
iteračných princípoch (pozri kapitolu Reálne čísla,
paragraf
Algoritmy).
Budú nás zaujímať hlavne dve základné otázky:
- Konverguje postupnosť vytvorená danou iteračnou metódou?
- Ak konverguje, tak ako rýchlo?
Ak konverguje postupnosť vytvorená danou iteračnou metódou,
hovoríme,
že iteračná metóda konverguje.
Ak o koreni rovnice vieme len toľko, že leží v intervale
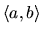 a nemáme žiadne
iné informácie o jeho polohe, použijeme iteračnú metódu, ktorej konvergencia
nezávisí od voµby začiatočnej aproximácie. Takéto metódy voláme
vždy konvergentné metódy. Spravidla majú tú nevýhodu,
že konvergujú pomaly, a preto sú zvyčajne vhodné pre
určenie takej aproximácie koreňa,
ktorá by mohla slúžiť ako začiatočná aproximácia
pre nejakú rýchlo konvergentnú metódu, ktorá ale vyžaduje "dobrú" počiatočnú aproximáciu
koreňa. Preto metódy riešenia nelineárnych rovníc rozdeľujeme na dva typy:
a nemáme žiadne
iné informácie o jeho polohe, použijeme iteračnú metódu, ktorej konvergencia
nezávisí od voµby začiatočnej aproximácie. Takéto metódy voláme
vždy konvergentné metódy. Spravidla majú tú nevýhodu,
že konvergujú pomaly, a preto sú zvyčajne vhodné pre
určenie takej aproximácie koreňa,
ktorá by mohla slúžiť ako začiatočná aproximácia
pre nejakú rýchlo konvergentnú metódu, ktorá ale vyžaduje "dobrú" počiatočnú aproximáciu
koreňa. Preto metódy riešenia nelineárnych rovníc rozdeľujeme na dva typy:
- štartovacie metódy
- spresňujúce metódy
Neznamená to však, že štartovacia metóda konverguje vždy pomaly a spresňujúca
zas konverguje vždy rýchlo. Závisí to vždy od
konkrétnej situácie a vlastností funkcie
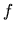 .
.
V ďalšom budeme predpokladať, že funkcia 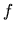 , ktorej koreň na intervale
, ktorej koreň na intervale
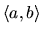 hľadáme, je na tomto intervale spojitá.
K tomu, aby sme mohli odpovedať na druhú otázku z dvoch
vyššie položených, zavedieme najskôr nasledujúci pojem:
hľadáme, je na tomto intervale spojitá.
K tomu, aby sme mohli odpovedať na druhú otázku z dvoch
vyššie položených, zavedieme najskôr nasledujúci pojem:
Hovoríme, že postupnosť 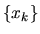 konverguje k číslu
konverguje k číslu 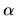 s
rýchlosťou rádu r, ak pre
s
rýchlosťou rádu r, ak pre
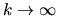 platí:
Existuje taká konštanta
platí:
Existuje taká konštanta 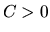 , že
, že
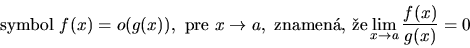 |
(7.5) |
Subsections
![]() , definovaná na intervale
, definovaná na intervale
![]() .
Chceme nájsť reálne číslo
.
Chceme nájsť reálne číslo
![]() (pokiaľ existuje),
pre ktoré platí
(pokiaľ existuje),
pre ktoré platí