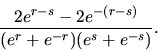Hyperbolický sínus je funkcia
Je to nepárna rastúca neohraničená funkcia.
Obrázok:
Graf funkcie 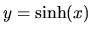
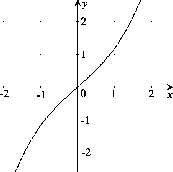 |
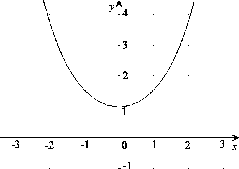
Hyperbolický kosínus je funkcia
Je to zdola ohraničená párna funkcia.
Obrázok:
Graf funkcie 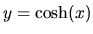
 |
Hyperbolický tangens je funkcia
Je to nepárna rastúca ohraničená funkcia.
Obrázok:
Graf funkcie
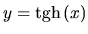
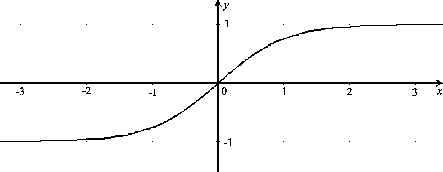 |
Hyperbolický kotangens je funkcia
Táto funkcia nie je definovaná v bode 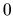 . Je nepárna neohraničená,
klesajúca v intervaloch
. Je nepárna neohraničená,
klesajúca v intervaloch 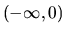 a
a 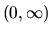 .
.
Obrázok:
Graf funkcie
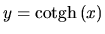
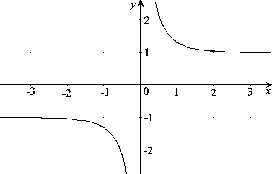 |
Hyperbolické funkcie nie sú periodické.
Príklad 15.
Ukážeme spomínané vlastnosti hyperbolického tangensu.
Riešenie:
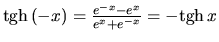 , preto je
to funkcia nepárna.
, preto je
to funkcia nepárna.
Funkcia 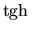 je rastúca, ak pre ľubovoľné
je rastúca, ak pre ľubovoľné 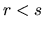 platí
platí
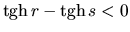 . Nech teda
. Nech teda 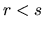 . Počítajme
. Počítajme
Menovateľ posledného zlomku je kladné číslo a čitateľ (pretože
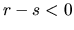 , odôvodnite!) je záporný, celý zlomok je teda záporný a
, odôvodnite!) je záporný, celý zlomok je teda záporný a
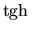 je rastúca funkcia.
je rastúca funkcia.
Pretože 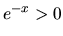 , platí
, platí
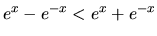 , teda
, teda
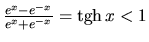 . Podobne sa dá
ukázať, že
. Podobne sa dá
ukázať, že
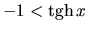 a preto
a preto 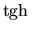 je ohraničená funkcia.
je ohraničená funkcia.

![]() , preto je
to funkcia nepárna.
, preto je
to funkcia nepárna.
![]() je rastúca, ak pre ľubovoľné
je rastúca, ak pre ľubovoľné ![]() platí
platí
![]() . Nech teda
. Nech teda ![]() . Počítajme
. Počítajme