Súčet, súčin, rozdiel aj podiel (ak existuje) dvoch periodických
funkcií s rovnakou periódou  je periodická funkcia. (Čo môžeme
povedať o jej perióde?)
Zložená funkcia je periodická, ak je periodická jej vnútorná
zložka.
je periodická funkcia. (Čo môžeme
povedať o jej perióde?)
Zložená funkcia je periodická, ak je periodická jej vnútorná
zložka.
Premyslite si: Funkcie 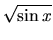 a
a 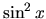 sú periodické
(zistite ich periódu), ale funkcie
sú periodické
(zistite ich periódu), ale funkcie 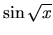 a
a 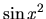 periodické nie sú.
periodické nie sú.
Periodická funkcia nemôže mať inverznú funkciu. (Prečo?)
Príklad 10.
Načrtnime graf ľubovoľnej funkcie, ktorá je neohraničená
zdola, rastie v intervale 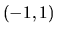 , klesá v intervale
, klesá v intervale 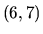 a je
periodická s periódou
a je
periodická s periódou 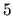 .
.
Riešenie: Stačí načrtnúť graf hľadanej funkcie v ľubovoľnom intervale
dĺžky 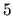 a potom ho periodicky rozšíriť. Zvoľme interval
a potom ho periodicky rozšíriť. Zvoľme interval
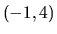 . Načrtneme rastúci graf v intervale
. Načrtneme rastúci graf v intervale 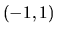 a klesajúci
v intervale
a klesajúci
v intervale 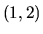 (prečo?), pričom v ľavom okolí čísla
(prečo?), pričom v ľavom okolí čísla 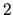 necháme
graf strmo klesať do
necháme
graf strmo klesať do 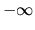 , aby sme splnili podmienku
neohraničenosti zdola. V intervale
, aby sme splnili podmienku
neohraničenosti zdola. V intervale 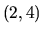 môžeme graf načrtnúť
ľubovoľne, pretože všetky podmienky sú splnené.
môžeme graf načrtnúť
ľubovoľne, pretože všetky podmienky sú splnené.
Obrázok:
Graf funkcie, ktorá spĺňa podmienky príkladu 10
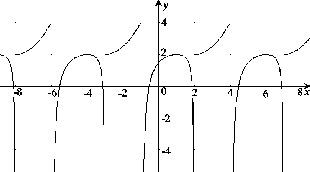 |

Príklad 11.
Popíšme vlastnosti funkcií určených nasledujúcimi rovnicami
Riešenie:
Nech 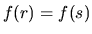 , teda
, teda
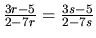 .
Po vynásobení obidvomi menovateľmi a úpravách dostaneme
.
Po vynásobení obidvomi menovateľmi a úpravách dostaneme
z čoho po ďalších úpravách vyplýva 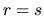 , teda
, teda 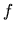 je prostá.
Nech
je prostá.
Nech 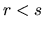 sú z
sú z
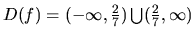 .
Nerovnica
.
Nerovnica 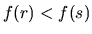 , t.j.
, t.j.
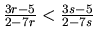 je ekvivalentná s nerovnicou
je ekvivalentná s nerovnicou
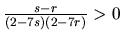 , ktorá
platí, ak obidve čísla
, ktorá
platí, ak obidve čísla 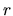 a
a 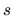 sú v tom istom intervale, z ktorých
sa skladá
sú v tom istom intervale, z ktorých
sa skladá 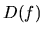 . Funkcia
. Funkcia 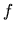 je teda rastúca v obidvoch intervaloch
je teda rastúca v obidvoch intervaloch
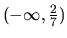 a
a
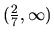 , ale nie je rastúca
(prečo ?). Kvôli určeniu ohraničenosti prepíšme pravidlo určujúce
funkciu
, ale nie je rastúca
(prečo ?). Kvôli určeniu ohraničenosti prepíšme pravidlo určujúce
funkciu
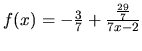 . Prvý člen
neovplyvní ohraničenosť, pre hodnoty
. Prvý člen
neovplyvní ohraničenosť, pre hodnoty 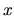 blízke číslu
blízke číslu
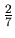 nadobúda druhý výraz ľubovoľne malé záporné hodnoty, ak
nadobúda druhý výraz ľubovoľne malé záporné hodnoty, ak
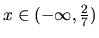 a ľubovoľne veľké kladné hodnoty, ak
a ľubovoľne veľké kladné hodnoty, ak
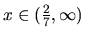 , funkcia nie je ohraničená, nemá teda ani
maximum ani minimum. Ďalej
, funkcia nie je ohraničená, nemá teda ani
maximum ani minimum. Ďalej
funkcia teda nie je párna, ani nepárna, takisto nie je periodická.
Funkcia
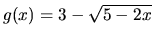 je zložená z troch funkcií
je zložená z troch funkcií
Platí
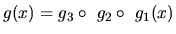 . Pretože všetky tri
funkcie sú prosté (to si ľahko overíte),
. Pretože všetky tri
funkcie sú prosté (to si ľahko overíte), 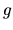 je prostá. Funkcie
je prostá. Funkcie
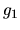 a
a 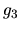 sú klesajúce a funkcia
sú klesajúce a funkcia 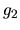 je rastúca, preto
výsledná funkcia je rastúca. Pretože
je rastúca, preto
výsledná funkcia je rastúca. Pretože
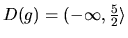 a
a 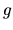 je rastúca, nadobúda v bode
je rastúca, nadobúda v bode
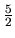 maximálnu hodnotu
maximálnu hodnotu 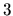 a je zhora ohraničená. Pre čísla
a je zhora ohraničená. Pre čísla 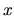 "blízke"
"blízke" 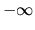 je
je 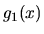 "blízke"
"blízke" 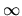 ,
,
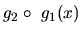 taktiež a následne
taktiež a následne 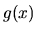 je "blízke"
je "blízke" 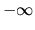 .
Preto
.
Preto 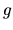 nie je ohraničená zdola. V dôsledku svojho definičného
oboru nemôže byť ani párna ani nepárna a ani periodická.
nie je ohraničená zdola. V dôsledku svojho definičného
oboru nemôže byť ani párna ani nepárna a ani periodická.
Keďže graf kvadratickej funkcie je ľahké načrtnúť, vlastnosti funkcie
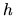 vyčítame z jej grafu.
vyčítame z jej grafu. 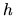 nie je prostá, klesá v intervale
nie je prostá, klesá v intervale
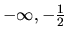 a rastie v intervale
a rastie v intervale
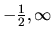 . Je zdola
ohraničená s minimom
. Je zdola
ohraničená s minimom 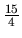 v bode
v bode 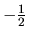 a zhora
neohraničená. Nemá žiadnu z vlastností symetrie, jej graf je však
symetrický podľa priamky
a zhora
neohraničená. Nemá žiadnu z vlastností symetrie, jej graf je však
symetrický podľa priamky 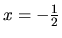 .
.

Ako sme sa mohli presvedčiť, niekedy je určovanie vlastností funkcie
(aj pomerne jednoduchej) dosť komplikované. Najjednoduchšie je
mať predstavu o jej grafe.
V nasledujúcej kapitole sú popísané efektívnejšie
techniky na určovanie vlastností funkcií.
![]() , klesá v intervale
, klesá v intervale ![]() a je
periodická s periódou
a je
periodická s periódou ![]() .
.
![]() a potom ho periodicky rozšíriť. Zvoľme interval
a potom ho periodicky rozšíriť. Zvoľme interval
![]() . Načrtneme rastúci graf v intervale
. Načrtneme rastúci graf v intervale ![]() a klesajúci
v intervale
a klesajúci
v intervale ![]() (prečo?), pričom v ľavom okolí čísla
(prečo?), pričom v ľavom okolí čísla ![]() necháme
graf strmo klesať do
necháme
graf strmo klesať do ![]() , aby sme splnili podmienku
neohraničenosti zdola. V intervale
, aby sme splnili podmienku
neohraničenosti zdola. V intervale ![]() môžeme graf načrtnúť
ľubovoľne, pretože všetky podmienky sú splnené.
môžeme graf načrtnúť
ľubovoľne, pretože všetky podmienky sú splnené.
![]()
![]() , teda
, teda
![]() .
Po vynásobení obidvomi menovateľmi a úpravách dostaneme
.
Po vynásobení obidvomi menovateľmi a úpravách dostaneme
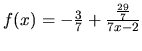 . Prvý člen
neovplyvní ohraničenosť, pre hodnoty
. Prvý člen
neovplyvní ohraničenosť, pre hodnoty