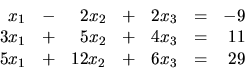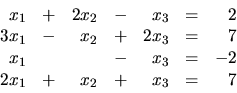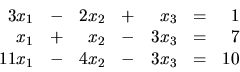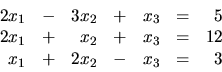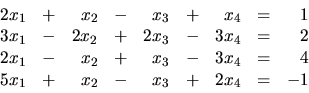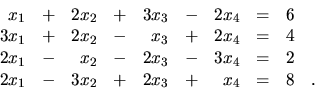1. Zistite, či
1.
Zistite, či ![]() ,
, ![]() je riešením sústavy rovníc
je riešením sústavy rovníc
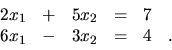
2.
Zistite, či vektory ![]() ,
, ![]() ,
, ![]() sú riešením sústavy rovníc
sú riešením sústavy rovníc
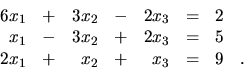
3.
Zistite, či vektory ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() sú riešením sústavy rovníc
sú riešením sústavy rovníc
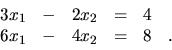
4.
Uveďte geometrickú interpretáciu sústavy dvoch lineárnych rovníc
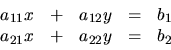
5.
Napíšte sústavy dvoch lineárnych rovníc s dvomi neznámymi, ktoré majú
vlastnosť: a) má práve jedno riešenie , b) nemá riešenie , c) má
nekonečne veľa riešení .
6.
Vyriešte nasledovné sústavy lineárnych rovníc
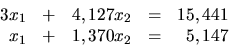
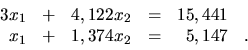
7. Použitím Frobeniusovej vety zistite, či nasledovné sústavy
lineárnych rovníc sú riešiteľné:
a)