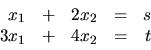Úvod

Z predchádzajúcej kapitoly už vieme, čo je matica. Matice typu $1\times n$ a $n\times 1$ nazývame vektory (riadkové, stĺpcové). Tento pojem logicky nadväzuje a rozširuje pojem vektora definovaného v kapitole 2.

Nech $m,n\in {\bf N}$, $a_{ij}\in {\bf R}$ pre $i=1,\ldots ,m$, $j=1,\ldots ,n$, $b_i\in {\bf R}$ pre $i=1,\ldots ,m$ sú dané čísla. Potom sústavou m lineárnych rovníc s n neznámymi $x_1,x_2,\ldots,x_n$ nazývame systém rovníc

$$a_{11}x_1 + \ldots \hspace{3mm} + a_{1n}x_n = b_1$$

$$a_{21}x_1 + \ldots \hspace{3mm} + a_{2n}x_n = b_2$$

$$\vdots \vdots \ \ \ \vdots$$ (4.1)

$$a_{m1}x_1 + \ldots \hspace{3mm} + a_{mn}x_n = b_m.$$

Jednotlivé rovnice sú matematickým vyjadrením podmienok, ktorým musia vyhovovať neznáme $x_1$, $x_2$,...,$x_n$. To, že sa jedná o sústavu rovníc znamená, že tieto podmienky musia byť splnené súčasne. V súlade so stredoškolskou terminológiou sa pri malom počte neznámych tieto niekedy označujú ako $x$, $y$ prípadne $z$.

Riešením sústavy (4.1) nazývame $n$ reálnych čísel $r_1,r_2,\ldots,r_n$ tej vlastnosti, že po ich dosadení za $x_1,x_2,\ldots,x_n$ v (4.1) dostaneme $m$ platných rovností medzi číslami.

Riešiť sústavu (4.1) znamená nájsť všetky riešenia tejto sústavy.

Ak definujeme maticu A typu $m\times n$ s prvkami $a_{ij}$ pre $i=1,\ldots ,m$, $j=1,\ldots ,n$, A =$(a_{ij})$ , vektory x, b typu $n\times 1$ resp. $m\times 1$ takto:

$${\bf x}={(x_1, \ldots ,x_n)}^T ,{\bf b}={(b_1, \ldots ,b_m)}^T,$$

tak môžeme sústavu (4.1) zapísať v tvare

$${\bf { Ax=b}. }$$ (4.2)

Maticu A nazývame matica sústavy (4.1) , vektor b tiež pravá strana sústavy (4.1).

Riešením (4.2) nazývame vektor ${\bf r}={{(r_1, \ldots ,r_n)} ^T}$, pre ktorý platí rovnosť vektorov ${ \bf { Ar }}$ a ${ \bf b}$.

Zápisy sústavy v tvare (4.1) a (4.2) sú zrejme ekvivalentné.

Maticu

$$\left( \begin{array}{ccccc} a_{11} & a_{12} & \ldots & a_... ...{m1} & a_{m2} & \ldots & a_{mn} & b_m \\ \end{array} \right)$$ (4.3)

nazývame rozšírená matica sústavy (4.1) a označujeme ju ( ${\bf A \mid \bf b}$).

Medzi číslami $m$ a $n$ nie je vo všeobecnosti žiadny súvis. Ak $m > n$,tak sústava rovníc sa nazýva preurčená. Ak $m < n$,tak sústava rovníc sa nazýva nedourčená. Ak v (4.1) je $b_1=b_2= \ldots =b_m=0$, tak odpovedajúcu sústavu $m$ lineárnych rovníc o $n$ neznámych nazývame homogénna sústava rovníc. Je teda tvaru

$${\bf { Ax=0}. }$$ (4.4)

Hned vidieť, že táto sústava rovníc má vždy riešenie $r_1=0$, $r_2=0$, ...,$r_n=0$, t. j. nulový vektor

$${\bf r}={(0,0, \ldots ,0)}^T.$$

Takéto riešenie nazývame triviálnym riešením (4.4).

Už na sústave dvoch lineárnych rovníc o dvoch neznámych sa dajú demonštrovať všetky možnosti týkajúce sa riešiteľnosti, ktoré môžu nastať pre sústavu (4.1). Pre sústavu (4.1) môže nastať práve jedna z týchto možností:

• má práve jedno riešenie
• má nekonečne veľa riešení
• nemá žiadne riešenie.

Základným teoretickým výsledkom týkajúcim sa riešiteľnosti (4.1) je nasledujúca Frobeniusova veta.
Sústava (4.1) ma riešenie práve vtedy, ak hodnosť matice sústavy je rovná hodnosti rozšírenej matice sústavy, t. j. ak platí

$h({\bf A }) = h({\bf A\vert b}).$

Vzhľadom na to, že hodnosť matice už viete určiť, tak iba uvedieme, že nezisťujeme zvlášť hodnosť matice sústavy a zvlášť hodnosť rozšírenej matice sústavy. Pracujeme iba s rozšírenou maticou sústavy, pričom si v nej pre prehľad oddelíme posledný stĺpec zvislou čiarou (odtiaľ pochádza aj označenie (${\bf A\vert b}$).

Príklad 1. Zistite, či sústava rovníc

$$\begin{array}{rrrrr} -2x_1 & + & x_2 & = & -1 \\ x_1 & + & 2x_2 & = & 1 \\ -6x_1 & + & 3x_2 & = & 3 \\ \end{array}$$

je riešiteľná.

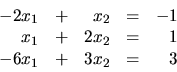
Riešenie: Budeme pracovať s ``maticou"

$$\left( \begin{array}{rr} -2 & 1\\ 1 & 2\\ -6 & 3\\ ... ...ft. \begin{array}{r} -1\\ 1\\ 3\\ \end{array} \right)$$

a zisťujeme jej hodnosť. Známym spôsobom postupne dostávame:

$${ { \left( \begin{array}{rr} -2 & 1\\ 1 & 2\\ -6 & 3\... ...gin{array}{r} 1\\ 3\\ -2 \\ \end{array} \right). } }$$

Teda $h({\bf A}) = 2$, $h({\bf A\vert b}) = 3$ . Nakoľko $2 \neq 3$, sústava nie je riešiteľná. $\clubsuit$

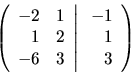
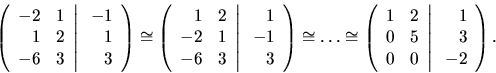
Zovšeobecnením sústavy (4.1) je sústava m lineárnych rovníc s n neznámymi s parametrom (parametrami). Ku takejto sústave sa dostaneme vtedy, ak niektorý ( alebo niektoré ) z koeficientov $a_{ij} , b_i$ závisí známym spôsobom od istého parametra, a teda môže nadobúdať nekonečne veľa alebo iba konečne veľa reálnych hodnôt. Môže nás zaujímať, ako tento parameter ovplyvňuje riešenie sústavy, riešiteľnosť sústavy alebo počet riešení sústavy atď.

Parametre budeme v dalšom označovať $s$, $t$, $u$.

Typický príklad by teda mohol byť:vyšetriť, ako zavisí riešenie sústavy rovníc

$$\begin{array}{rrrrr} x_1 & + & 2x_2 & = & s \\ 3x_1 & + & 4x_2 & = & t \\ \end{array}$$

$s ,\, t \in {\bf R}$, na hodnotách $s ,\, t$. Ak by sme takýto vzťah našli, tak postupným dosadzovaním potrebných hodnôt parametrov $s ,\, t$ dostávame odpovedajúce riešenia. Sústava s parametrom je vo všeobecnosti teda zložitejší problém ako sústava (4.1) Frobeniusovu vetu môžeme samozrejme použiť aj pre sústavu s parametrom. Následná analýza riešiteľnosti však može byť značne náročná.