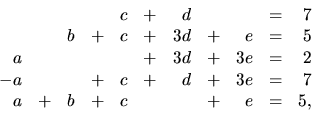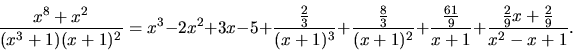Racionálna funkcia je funkcia definovaná rovnicou
kde 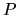 a
a 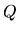 sú polynómy. Jej definičný obor je množina všetkých
čísel
sú polynómy. Jej definičný obor je množina všetkých
čísel 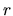 , pre ktoré
, pre ktoré 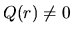 . V prípade, ak stupeň polynómu
. V prípade, ak stupeň polynómu
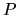 je menší ako stupeň polynómu
je menší ako stupeň polynómu 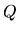 , hovoríme o
rýdzo racionálnej funkcii. Všeobecné vlastnosti a grafy
racionálnych funkcií je ťažké popísať. Pri práci s nimi je často
dôležité rozložiť danú racionálnu funkciu na súčet
elementárnych (parciálnych) zlomkov. Pritom postupujeme
podľa nasledujúceho návodu.
, hovoríme o
rýdzo racionálnej funkcii. Všeobecné vlastnosti a grafy
racionálnych funkcií je ťažké popísať. Pri práci s nimi je často
dôležité rozložiť danú racionálnu funkciu na súčet
elementárnych (parciálnych) zlomkov. Pritom postupujeme
podľa nasledujúceho návodu.
- Vydelením mnohočlenov
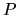 a
a 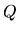 prepíšeme funkciu na súčet
mnohočlena a rýdzo racionálnej funkcie.
prepíšeme funkciu na súčet
mnohočlena a rýdzo racionálnej funkcie.
- Mnohočlen
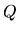 v menovateli rozložíme na súčin koreňových
činiteľov.
v menovateli rozložíme na súčin koreňových
činiteľov.
- Ku každému činiteľu typu
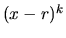 vytvoríme práve
vytvoríme práve 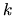 zlomkov
zlomkov
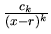 ,
,
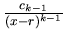 ,
...,
,
...,
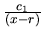 .
.
- Ku každému činiteľu typu
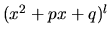 vytvoríme práve
vytvoríme práve
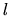 zlomkov
zlomkov
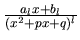 ,
,
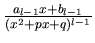 ,
,
...,
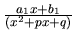 .
.
- Neznáme koeficienty vypočítame porovnaním rýdzo racionálnej
časti a súčtu všetkých elementárnych zlomkov.
- Pôvodná funkcia sa rovná súčtu mnohočlenu, ktorý sme dostali
delením so súčtom všetkých elementárnych zlomkov.
Príklad 13.
Rozložme na súčet elementárnych zlomkov funkciu
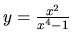 .
.
Riešenie: Postupujeme podľa návodu.
- Pretože daná funkcia je rýdzo racionálna, prvú časť postupu
vynecháme.
-
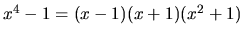 ,
,
- vytvoríme elemntárne zlomky
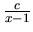 ,
, 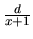 ,
,
- a zlomok
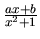 .
.
- Porovnáme
Pretože menovatele sa rovnajú, rovnajú sa aj čitatele a teda
Po roznásobení a úprave pravej strany dostávame rovnosť dvoch
mnohočlenov
Pretože dva mnohočleny sa rovnajú práve vtedy, ak majú zhodné všetky
koeficienty, posledná rovnosť je ekvivalentná so sústavou lineárnych
rovníc
ktorá má riešenie
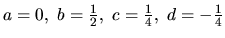 .
.
- Preto platí

Príklad 14.
Rozložme na súčet mnohočlena a elementárnych zlomkov funkciu
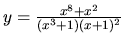 .
.
Riešenie:
- Keďže nejde o rýdzo racionálnu funkciu, mnohočleny najskôr
vydelíme. Dostaneme podiel
 a zvyšok
a zvyšok
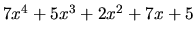 . Preto
. Preto
Rýdzo racionálnu časť funkcie ďalej rozložíme na súčet
elementárnych zlomkov.
- Mnohočlen v menovateli rozložíme na súčin koreňových činiteľov
pomocou rozkladu
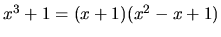 , ktorého kvadratický
činiteľ sa ďalej rozložiť nedá. Preto
, ktorého kvadratický
činiteľ sa ďalej rozložiť nedá. Preto
- vytvoríme elemntárne zlomky
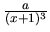 ,
,
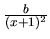 ,
, 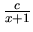
- a zlomok
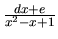 .
.
- Porovnáme
Po vynásobení menovateľom ľavej strany a úprave pravej strany
dostávame rovnosť dvoch mnohočlenov
Porovnaním koeficientov pri rovnakých mocninách premennej 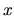 dostávame
sústavu lineárnych rovníc
dostávame
sústavu lineárnych rovníc
ktorá má riešenie
- Preto platí

Najdôležitejší špeciálny typ racionálnej funkcie je
Subsections
![]() .
.
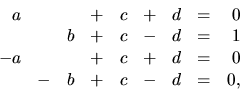
![]() .
.