V časti o využití inverznej matice sme riešili aj úlohy typu AX=B pre vhodné definované matice A, X, B.
Ku takejto rovnici by sme sa dostali, ak by sme potrebovali riešiť
istý počet sústav s jednou maticou sústavy, ale s rôznymi pravými
stranami:
Ak A je regulárna matica, tak prvá myšlienka by bola určiť
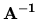 a odpovedajúce riešenia dostať v tvare:
a odpovedajúce riešenia dostať v tvare:
Podrobná analýza však ukazuje, že je výhodnejšie použiť princíp GEM
aj na takúto úlohu.
Zo stĺpcových vektorov
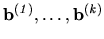 zostrojíme maticu
zostrojíme maticu
zapísaním jednotlivých stĺpcov za sebou. Vhodne označíme
neznáme a vytvoríme z nich maticu X. Dostaneme sa tak ku
maticovej rovnici AX=B. Ďalej je výhodné postupovať tak, ako
je uvedené v závere časti o GEM, t.j. pracovať iba s rozšírenou
maticou sústavy 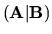 a využívať ekvivalentné úpravy
G1, G2, G3. Nesmieme zabudnúť na to, že na pravej strane máme viacero
stĺpcov, a preto treba každý z nich upravovať. Spätnou
substitúciou, pričom berieme do úvahy odpovedajúce si stĺpce
neznámych a pravých strán, dostaneme riešenie.
a využívať ekvivalentné úpravy
G1, G2, G3. Nesmieme zabudnúť na to, že na pravej strane máme viacero
stĺpcov, a preto treba každý z nich upravovať. Spätnou
substitúciou, pričom berieme do úvahy odpovedajúce si stĺpce
neznámych a pravých strán, dostaneme riešenie.
Príklad 12.
Riešte sústavy rovnic
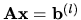 , ak
, ak
pre vektory pravých stran
Riešenie:
Ak označíme
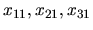 neznáme pre pravú stranu
neznáme pre pravú stranu
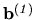 ,
,
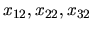 neznáme pre pravú stranu
neznáme pre pravú stranu
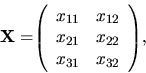
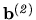 a vytvoríme z nich maticu X :
a vytvoríme z nich maticu X :
tak máme riešiť maticovú rovnicu AX = B. Napíšte si ju! Po
``odstránení"
neznámych dostaneme rozšírenú maticu tvaru:
Známymi úpravami dospejeme ku matici tvaru:
Ak by sme si zas ``pripísali" neznáme, tak od sústavy AX = B sme
sa dostali ku sústave CX = D . Urobte tak! Matica C má
vlastnosti požadované v GEM. Spätnou substitúciou, ak berieme do
úvahy prvý stĺpec matice D, dostaneme
a ak berieme do úvahy druhý stĺpec matice D, konečne dostaneme
Samozrejme, že sme mohli pokračovať až po redukovaný Gaussov tvar
matice A a nebolo by potrebné robiť spätnú substitúciu. Z
hľadiska počtu operácií to je však nevýhodné.

Na riešení maticovej rovnice AX = B, pre vhodnú voľbu matice
B, je založená jedna z metód na určenie 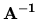 . Pre
inverznú maticu (predpokladáme, že existuje) platí
. Pre
inverznú maticu (predpokladáme, že existuje) platí
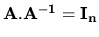 . Teda
. Teda 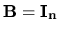 . Aby sa nemusela robiť spätná substitúcia,
je nutné upraviť maticu A na redukovaný Gaussov tvar. Potom už
vedľa nej napísaná matica je inverznou maticou ku matici A. Príklad na takýto postup bol uvedený v časti 3.1.7 o
určovaní inverznej matice.
. Aby sa nemusela robiť spätná substitúcia,
je nutné upraviť maticu A na redukovaný Gaussov tvar. Potom už
vedľa nej napísaná matica je inverznou maticou ku matici A. Príklad na takýto postup bol uvedený v časti 3.1.7 o
určovaní inverznej matice.
![]() zostrojíme maticu
zostrojíme maticu
![]() , ak
, ak
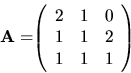
![]() neznáme pre pravú stranu
neznáme pre pravú stranu
![]() ,
,
![]() neznáme pre pravú stranu
neznáme pre pravú stranu
![]() a vytvoríme z nich maticu X :
a vytvoríme z nich maticu X :
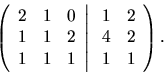
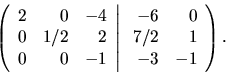
![]() . Pre
inverznú maticu (predpokladáme, že existuje) platí
. Pre
inverznú maticu (predpokladáme, že existuje) platí
![]() . Teda
. Teda ![]() . Aby sa nemusela robiť spätná substitúcia,
je nutné upraviť maticu A na redukovaný Gaussov tvar. Potom už
vedľa nej napísaná matica je inverznou maticou ku matici A. Príklad na takýto postup bol uvedený v časti 3.1.7 o
určovaní inverznej matice.
. Aby sa nemusela robiť spätná substitúcia,
je nutné upraviť maticu A na redukovaný Gaussov tvar. Potom už
vedľa nej napísaná matica je inverznou maticou ku matici A. Príklad na takýto postup bol uvedený v časti 3.1.7 o
určovaní inverznej matice.