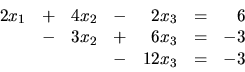
Príklad 10.
Zistite, či sústava lineárnych rovníc
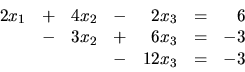
Riešenie:
Determinant odpovedajúcej matice sústavy je
![]() , a
preto má sústava jediné riešenie. Iste ste si všimli, že z poslednej
rovnice ľahko dostávame
, a
preto má sústava jediné riešenie. Iste ste si všimli, že z poslednej
rovnice ľahko dostávame ![]() /
/![]() . Z predposlednej potom
platí
. Z predposlednej potom
platí
![]() , a teda
, a teda ![]() . Konečne z prvej rovnice
dostávame, že
. Konečne z prvej rovnice
dostávame, že ![]() . Potom
. Potom
![]() .
.
![]()
Tento spôsob riešenia sústavy rovníc takéhoto tvaru sa nazýva spätná substitúcia.
Sústavy lineárnych rovníc Ax = b , Cx = d sa nazývajú ekvivalentné , ak každé riešenie sústavy Ax = b je riešením sústavy Cx = d a každé riešenie sústavy Cx = d je riešením sústavy Ax = b . Prechod od sústavy Ax = b ku ekvivalentnej sústave Cx = d realizujeme pomocou ekvivalentných úprav.
Uvažujme opäť o sústave (4.5). Gaussova eliminačná
metoda (GEM) riešenia sústavy (4.5) je založená na tom, že od
sústavy lineárnych rovníc Ax = b prejdeme ku ekvivalentnej sústave
rovníc Cx = d , pričom matica C má vlastnosť
Ekvivalentné úpravy, ktoré používame pri GEM sú:
Príklad 11.
GEM riešte sústavu
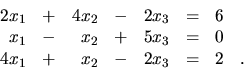
Riešenie:
Pretože
![]() (presvedčte sa ), má sústava práve jedno
riešenie. Pomocou ekvivalentných úprav chceme dospieť ku sústave Cx = d ,
pričom matica C bude mať štruktúru:
(presvedčte sa ), má sústava práve jedno
riešenie. Pomocou ekvivalentných úprav chceme dospieť ku sústave Cx = d ,
pričom matica C bude mať štruktúru:

Vynásobme prvú rovnicu sústavy číslom ![]() a pripočítajme ju ku
druhej rovnici. Dostaneme sústavu
a pripočítajme ju ku
druhej rovnici. Dostaneme sústavu
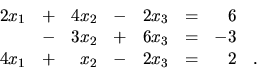
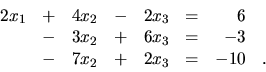
Vynásobením druhej rovnice číslom ![]() a pripočítaním ku tretej
rovnici konečne dostaneme
a pripočítaním ku tretej
rovnici konečne dostaneme
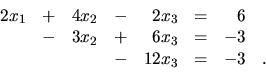
Vráťme sa ku všeobecnej sústave (4.5). Sformulujeme všeobecnú stratégiu pri GEM.
Prepokladajme, že prvok ![]() . Pripočítaním vhodných
násobkov prvej rovnice ku zostávajúcim
. Pripočítaním vhodných
násobkov prvej rovnice ku zostávajúcim ![]() rovniciam dosiahneme,
že koeficienty pri
rovniciam dosiahneme,
že koeficienty pri ![]() v týchto rovniciach budú
nulové. Postupne budeme prvú rovnicu násobiť číslami
v týchto rovniciach budú
nulové. Postupne budeme prvú rovnicu násobiť číslami
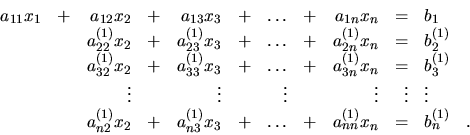
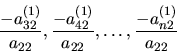
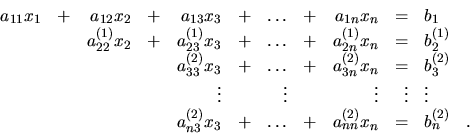
Za predpokladu,že

Čísla
![]() pre
pre
![]() nazývame
pivot
nazývame
pivot ![]() -teho kroku GEM. Pritom
-teho kroku GEM. Pritom
![]() .
.
Existujú dve triedy matíc A, pre ktoré takto popísaná GEM je realizovateľná.
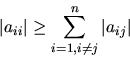
(Ak pre aspoň jedno ![]() platí
platí
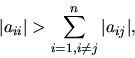
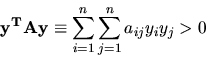
Diagonálna dominantnosť je ľahko verifikovateľná. O mnohých sústavách lineárnych rovníc, ktoré vznikajú pri riešení praktických problémov sa vie, že matica sústavy je kladne definitná, prípadne je známa podmienka, väčšinou ľahko splniteľná na to, aby matica sústavy bola kladne definitná.
Sústavu lineárnych rovníc
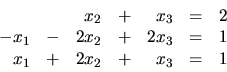
Pri použití GEM nie je nutné preverovať podmienku, či
![]() . Na základe známych vlastností determinantov platí: ak
. Na základe známych vlastností determinantov platí: ak
![]() , tak aj
, tak aj
![]() . (A teda, ak
. (A teda, ak ![]() , tak aj
, tak aj
![]() . )Pre regulárnosť matice A je totiž podstatné
iba to, že
. )Pre regulárnosť matice A je totiž podstatné
iba to, že
![]() a nie akú má nenulovú hodnotu.
a nie akú má nenulovú hodnotu.
Ekvivalentné úpravy G1, G2, G3 nápadne pripomínajú riadkové operácie
O1, O2, O3, ktoré sa používali pri vytvorení Gaussovho tvaru
matice. Stačí len ``zrušiť" neznáme
![]() a pracovať
s rozšírenou maticou
a pracovať
s rozšírenou maticou ![]() . Po nájdení jej Gaussovho tvaru
je potrebné zas ``pripísať si" neznáme
. Po nájdení jej Gaussovho tvaru
je potrebné zas ``pripísať si" neznáme
![]() za
odpovedajúce koeficienty a máme sústavu Cx = d . Technický
rozdiel, (ktorý
ale vymizne, ak použijeme spätnú substitúciu), je ten, že Gaussov tvar
matice vyžadoval vedúce jednotky, kým GEM vyžaduje, aby vedúce prvky
(pivoty) ako analógie vedúcich jednotiek boli rôzne od
nuly. Samozrejme, že použitím G2 by sme dosiahli, aby boli jednotkami.
za
odpovedajúce koeficienty a máme sústavu Cx = d . Technický
rozdiel, (ktorý
ale vymizne, ak použijeme spätnú substitúciu), je ten, že Gaussov tvar
matice vyžadoval vedúce jednotky, kým GEM vyžaduje, aby vedúce prvky
(pivoty) ako analógie vedúcich jednotiek boli rôzne od
nuly. Samozrejme, že použitím G2 by sme dosiahli, aby boli jednotkami.
Jedna z modifikácií GEM sa nazýva Gaussova -- Jordanova
eliminačná metóda. Tá vyžaduje, aby sme sa od sústavy Ax = b cez sústavu
Cx = d dostali ku sústave Ex = f , pričom matica E je
diagonálna s ![]() . Súvis s redukovaným Gaussovým tvarom
matice je už zrejmý.
. Súvis s redukovaným Gaussovým tvarom
matice je už zrejmý.