Vzdialenosť dvoch daných bodov vypočítame podľa vzťahu (2.1).
Bežne sú známe jednoduché vzťahy na výpočet vzdialenosti bodu od
priamky v rovine a vzdialenosti bodu od roviny v priestore. Obidva
vzťahy sú navzájom veľmi podobné:
Vstupné informácie Výsledná vzdialenosť
Bod ![$X_{0} = [x_{0},y_{0}]$](img706.gif) a
a 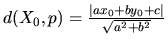
priamka  určená rovnicou
určená rovnicou 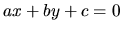
Bod ![$X_{0}=[x_{0},y_{0},z_{0}]$](img792.gif) a
a 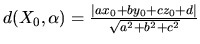
rovina 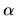 určená rovnicou
určená rovnicou 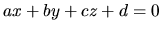
V obidvoch prípadoch čitateľ zlomku na pravej strane dostaneme tak, že
do príslušnej rovnice dosadíme súradnice príslušného bodu a vytvoríme absolútnu
hodnotu, v menovateli je dĺžka normálového vektora určeného koeficientami
príslušnej priamky, resp. roviny.
Príklad 26.
Vypočítame vzdialenosť bodu ![$P[-7,3]$](img873.gif) od priamky
od priamky
![$p:\ [x,y] = [-2+3t,1-t]$](img874.gif) .
.
Riešenie:
Najskôr nájdeme všeobecnú rovnicu priamky  . Jej normálové vektory
sú kolmé k jej smerovému vektoru
. Jej normálové vektory
sú kolmé k jej smerovému vektoru ![$[3,-1]$](img875.gif) , napríklad vektor
, napríklad vektor
![$\vec{n} = [1,3]$](img876.gif) . Preto všeobecná rovnica priamky
. Preto všeobecná rovnica priamky  po úprave je
po úprave je
Teraz použijeme vzťah pre vzdialenosť bodu od priamky v rovine

Príklad 27.
Rovina
pretína guľovú plochu
v kružnici 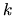 . Vypočítame polomer
kružnice
. Vypočítame polomer
kružnice 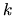 a napíšeme rovnicu dotykovej roviny
a napíšeme rovnicu dotykovej roviny 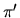 ku guľovej ploche
ku guľovej ploche
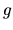 rovnobežnej s rovinou
rovnobežnej s rovinou 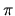 .
.
Riešenie:
Najskôr si určíme vzdialenosť stredu ![$S[2,-3,-4]$](img883.gif) guľovej plochy od
roviny
guľovej plochy od
roviny 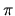
Označme hľadaný polomer 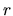 , stred kružnice
, stred kružnice 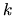 znakom
znakom 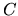 a zvoľme
ľubovoľný bod
a zvoľme
ľubovoľný bod 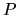 na kružnici
na kružnici 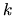 . Trojuholník
. Trojuholník 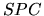 je pravuohlý s
pravým uhlom pri vrchole
je pravuohlý s
pravým uhlom pri vrchole 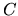 , odvesnami
, odvesnami 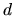 a
a 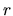 a preponou rovnou
polomeru guľovej plochy
a preponou rovnou
polomeru guľovej plochy 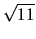 . Podľa Pytagorovej vety platí
. Podľa Pytagorovej vety platí
a
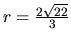 .
.
Keďže hľadaná rovina 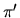 je rovnobežná s rovinou
je rovnobežná s rovinou 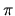 , jej rovnica
je
, jej rovnica
je
pre isté číslo 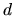 , ktoré máme nájsť. Keďže vzdialenosť stredu
, ktoré máme nájsť. Keďže vzdialenosť stredu 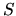 guľovej plochy od jej dotykovej roviny je rovná polomeru, dostávame
rovnicu
guľovej plochy od jej dotykovej roviny je rovná polomeru, dostávame
rovnicu
po úprave
s dvomi riešeniami 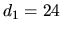 a
a 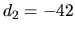 .
Hľadané roviny sú dve
.
Hľadané roviny sú dve

Vzdialenosť dvoch rovnobežných priamok v rovine určíme tak, že na
ľubovoľnej z nich určíme ľubovoľný bod a vypočítame jeho vzdialenosť od druhej
priamky.
Vzdialenosť dvoch rovnobežných rovín určíme tak, že na ľubovoľnej
z nich určíme ľubovoľný bod a vypočítame jeho vzdialenosť od druhej roviny.
Vzdialenosť priamky rovnobežnej s rovinou určíme tak, že na priamke
určíme ľubovoľný bod a vypočítame jeho vzdialenosť od roviny.
Vzdialenosť bodu od priamky v priestore je rovná vzdialenosti
tohoto bodu od jeho kolmého priemetu na danú priamku. Praktický
výpočet vzdialenosti bodu 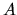 od priamky
od priamky  prevedieme v štyroch krokoch:
prevedieme v štyroch krokoch:
- Vyjadríme všeobecný vektor
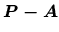 , kde
, kde 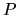 je ľubovoľný
bod priamky
je ľubovoľný
bod priamky 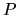 v závislosti od parametra priamky,
v závislosti od parametra priamky,
- nájdeme tú (jedinú) hodnotu parametra, pre ktorú je tento
vektor kolmý na smerový vektor priamky
 ,
,
- dosadíme vypočítanú hodnotu parametra do vyjadrenia
všeobecného vektora,
- hľadaná vzdialenosť je rovná dĺžke takto získaného vektora.
Vzdialenosť dvoch rovnobežných priamok v priestore určíme tak, že
na ľubovoľnej z nich si zvolíme ľubovoľný bod a postupujeme podľa
predchádzajúceho prípadu.
Príklad 28.
Vypočítame vzdialenosť rovnobežných rovín
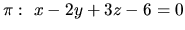 a
a
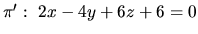 .
.
Riešenie:
Zvoľme napríklad
![$[-3,0,0] \in \pi'$](img899.gif) a vypočítajme jeho vzdialenosť
od
a vypočítajme jeho vzdialenosť
od 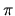

Príklad 29.
Vypočítame vzdialenosť bodu ![$Q[-2,3,1]$](img901.gif) od priamky
od priamky
![$p: [x,y,z] = [9 + 4t,-2 - t,$](img902.gif)
![$2 + 3t]$](img903.gif) .
.
Riešenie:
- Všeobecný vektor
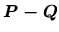 má vyjadrenie
má vyjadrenie
- Tento vektor je kolmý na smerový vektor
![$\vec{s}=[4,-1,3]$](img906.gif) priamky
priamky  práve vtedy, ak
práve vtedy, ak
Hľadaná hodnota parametra je preto 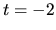 .
.
- Po dosadení dostávame súradnice konkrétneho vektora
- Hľadaná vzdialenosť je

Vzdialenosť dvoch mimobežných priamok určíme v štyroch krokoch:
- vyjadríme všeobecný vektor spájajúci ľubovoľný bod jednej priamky
s ľubovoľným bodom druhej priamky v závislosti od parametrov
obidvoch priamok,
- nájdeme tie (jednoznačne určené) hodnoty parametrov, pre ktoré
je tento vektor kolmý na smerové vektory obidvoch priamok,
- dosadíme takto získané parametre do vyjadrenia všeobecného
vektora,
- hľadaná vzdialenosť sa rovná dĺžke takto získaného vektora.
Príklad 30.
Vypočítame vzdialenosť prieniku  rovín
rovín
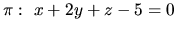 a
a
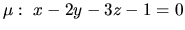 od priamky
od priamky
![$q:\ [x,y,z] = [-6+3t,-3,-2t]$](img912.gif) .
.
Riešenie:
Najskôr určíme vzájomnú polohu daných priamok. Smerový vektor
priamky  je kolmý na normálové vektory obidvoch rovín, ktoré
ju obsahujú. Je ním teda ľubovoľný násobok vektorového súčinu
je kolmý na normálové vektory obidvoch rovín, ktoré
ju obsahujú. Je ním teda ľubovoľný násobok vektorového súčinu
Kvôli jednoduchosti budeme pracovať s vektorom
Parametrické rovnice priamky  dostaneme voľbou ľubovoľného
spoločného bodu rovín
dostaneme voľbou ľubovoľného
spoločného bodu rovín 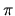 a
a 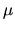 , napríklad bodu so súradnicami
, napríklad bodu so súradnicami
![$[5,-1,2]$](img916.gif)
Z rovníc priamok  a
a 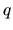 vidíme, že sú buď rôznobežné alebo
mimobežné. Priamka
vidíme, že sú buď rôznobežné alebo
mimobežné. Priamka 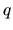 pretína rovinu
pretína rovinu 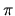 v bode so súradnicami
v bode so súradnicami
![$[45,-3,-34]$](img918.gif) , ktorý neleží v rovine
, ktorý neleží v rovine 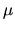 . Preto priamka
. Preto priamka 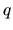 nepretína priamku
nepretína priamku  a obidve sú mimobežné.
a obidve sú mimobežné.
- Ak
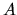 je ľubovoľný bod priamky
je ľubovoľný bod priamky  a
a 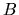 je ľubovoľný bod
priamky
je ľubovoľný bod
priamky 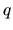 , tak vektor
, tak vektor 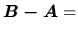
![$[-11+3t-s,-2+s,-2-2t-s]$](img920.gif) .
.
- Vektor
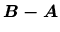 je kolmý na obidva smerové vektory
je kolmý na obidva smerové vektory
![$\vec{s_p} = [1,-1,1]$](img921.gif) a
a
![$\vec{s_q} = [3,0,-2]$](img922.gif) práve vtedy, ak
práve vtedy, ak
a súčasne
Po úprave a riešení sústavy rovníc dostaneme hodnoty 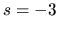 a
a
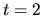 .
.
- Dosadením vypočítaných hodnôt parametrov dostávame konkrétny
vektor
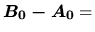
![$[-2,-5,-3]$](img928.gif) .
.
- Hľadaná vzdialenosť mimobežiek
 a
a 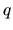 je
je

Na záver poznamenajme, že existujú aj iné spôsoby ako riešiť
vyššie popísané úlohy.
a
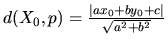
určená rovnicou
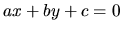
a
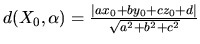
určená rovnicou
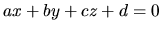
![]() od priamky
od priamky
![]() .
.
![]() . Jej normálové vektory
sú kolmé k jej smerovému vektoru
. Jej normálové vektory
sú kolmé k jej smerovému vektoru ![]() , napríklad vektor
, napríklad vektor
![]() . Preto všeobecná rovnica priamky
. Preto všeobecná rovnica priamky ![]() po úprave je
po úprave je
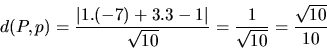
![]() guľovej plochy od
roviny
guľovej plochy od
roviny ![]()
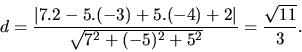
![]() od priamky
od priamky ![]() prevedieme v štyroch krokoch:
prevedieme v štyroch krokoch:
![]() a
a
![]() .
.
![]() a vypočítajme jeho vzdialenosť
od
a vypočítajme jeho vzdialenosť
od ![]()
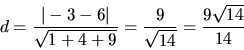
![]() od priamky
od priamky
![]()
![]() .
.
![]() rovín
rovín
![]() a
a
![]() od priamky
od priamky
![]() .
.
![]() je kolmý na normálové vektory obidvoch rovín, ktoré
ju obsahujú. Je ním teda ľubovoľný násobok vektorového súčinu
je kolmý na normálové vektory obidvoch rovín, ktoré
ju obsahujú. Je ním teda ľubovoľný násobok vektorového súčinu