1. Pomocou definície derivácie vypočítajte deriváciu funkcie
2. Pomocou definície derivácie vypočítajte deriváciu funkcie
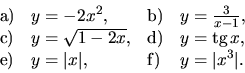
3. Vypočítajte deriváciu funkcie
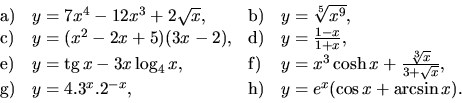
4. Vypočítajte deriváciu funkcie
![\begin{displaymath}
\begin{array}{llllll}
{\mathrm a)} & y = \cos 3x, & \hspace{...
...athrm l)} & y = \sqrt[5]{\frac{1}{\sqrt[3]{4x+1}}}.
\end{array}\end{displaymath}](img3362.gif)
5. Vypočítajte deriváciu inverznej funkcie k funkcii ![]() v bode
v bode
![]() bez určenia funkcie
bez určenia funkcie ![]()
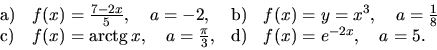
6. Vypočítajte deriváciu funkcie

7. Vypočítajte deriváciu implicitnej funkcie
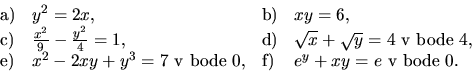
8. Vypočítajte deriváciu funkcie určenej parametrickými rovnicami
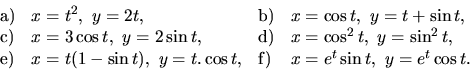
9. Dokážte, že ak má funkcia ![]() v bode
v bode ![]() deriváciu, tak je v
bode
deriváciu, tak je v
bode ![]() spojitá.
spojitá.
10. Predpokladajme, že funkcia ![]() má deriváciu. Dokážte, že platí
má deriváciu. Dokážte, že platí
11. Nájdite príklady funkcie ![]() , pre ktorú platí
, pre ktorú platí
12. Nájdite príklad funkcií ![]() a
a ![]() , pre ktoré platí
, pre ktoré platí
13. Nájdite príklad funkcie ![]() , pre ktorú platí
, pre ktorú platí
14. Vypočítajte derivácie funkcie do rádu ![]() pre danú hodnotu
pre danú hodnotu ![]()
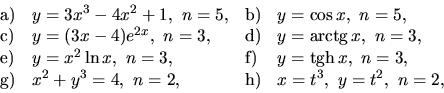
15. Vypočítajte derivácie funkcie rádu ![]() pre všeobecnú hodnotu
pre všeobecnú hodnotu
![]()

16. Nájdite rovnice dotyčnice a normály ku grafu funkcie ![]() v bode
v bode
![]()
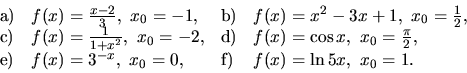
17. Nájdite rovnice dotyčnice a normály ku grafu funkcie ![]() rovnobežnej s priamkou
rovnobežnej s priamkou ![]()
18. Nájdite dotyčnicu s najväčšou smernicou ku grafu funkcie
![]() .
.
19. Nájdite rovnicu dotyčnice a normály ku elipse
![]() v bode
v bode ![]() .
.
20. Dotyčnica ku grafu funkcie určenej rovnicou ![]() vytvorí
spolu s osami
vytvorí
spolu s osami ![]() a
a ![]() trojuholník. Vyjadrite obsah tohoto
trojuholníka ako funkciu premennej
trojuholník. Vyjadrite obsah tohoto
trojuholníka ako funkciu premennej ![]() .
.
21. Asteroida je krivka určená rovnicou
![]() +
+ ![]() =
= ![]() . Dokážte, že úsečka
na dotyčnici ku asteroide ohraničená súradnicovými osami má
konštantú dĺžku
. Dokážte, že úsečka
na dotyčnici ku asteroide ohraničená súradnicovými osami má
konštantú dĺžku ![]() .
.
22. Teleso je vrhnuté zo zeme smerom kolmo nahor. Jeho výška po ![]() sekundách je (približne)
sekundách je (približne) ![]() metrov.
metrov.
23. Teleso sa pohybuje v smere osi ![]() , pričom jeho poloha v čase
, pričom jeho poloha v čase
![]() je daná vzťahom
je daná vzťahom
24. Človek výšky ![]() m sa vzďaľuje od zdroja svetla rýchlosťou
m sa vzďaľuje od zdroja svetla rýchlosťou
![]() . Zistite rýchlosť pohybu tieňa jeho hlavy, ak zdroj svetla
je umiestnený vo výške
. Zistite rýchlosť pohybu tieňa jeho hlavy, ak zdroj svetla
je umiestnený vo výške ![]() m.
m.
25. Nájdite diferenciál funkcie
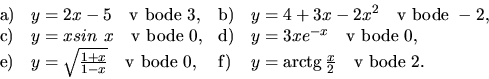
26. Použitím diferenciálu približne vypočítajte hodnoty
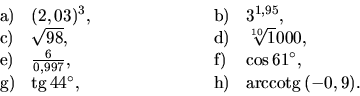
27. Pomocou diferenciálu odhadnite približne zmenu objemu gule pri
zmene jej polomeru ![]() o hodnotu
o hodnotu ![]() .
.
28. Hmotnosť platnej mince sa nesmie odlišovať o viac ako
![]() % od jej predpísanej hmotnosti. O koľko percent sa môže líšiť
polomer platnej mince od predpísaného polomeru za predpokladu, že
minca má predpísanú hrúbku.
% od jej predpísanej hmotnosti. O koľko percent sa môže líšiť
polomer platnej mince od predpísaného polomeru za predpokladu, že
minca má predpísanú hrúbku.
29. Perióda ![]() pohybu kyvadla je určená vzťahom
pohybu kyvadla je určená vzťahom
![]() , kde
, kde ![]() je dĺžka kyvadla v metroch,
je dĺžka kyvadla v metroch, ![]() je meraná v sekundách a
je meraná v sekundách a
![]() je gravitačná
konštanta. Použitím diferenciálu nájdite
je gravitačná
konštanta. Použitím diferenciálu nájdite
30. Nájdite Taylorov mnohočlen stupňa ![]() v bode
v bode ![]() pre funkciu
pre funkciu
31. Nech ![]() je Taylorov mnohočlen funkcie
je Taylorov mnohočlen funkcie ![]() stupňa
stupňa ![]() v bode
v bode
![]() a
a ![]() je Taylorov mnohočlen funkcie
je Taylorov mnohočlen funkcie ![]() stupňa
stupňa ![]() v bode
v bode ![]() .
Dokážte, že
.
Dokážte, že ![]() je Taylorov mnohočlen funkcie
je Taylorov mnohočlen funkcie ![]() stupňa
stupňa
![]() v bode
v bode ![]() .
.
32. Použite výsledok predchádzajúceho cvičenia na určenie Taylorovho
mnohočlenu stupňa ![]() funkcie
funkcie
![]() v bode
v bode ![]() pomocou Taylorových mnohočlenov funkcií
pomocou Taylorových mnohočlenov funkcií ![]() a
a ![]() .
.
33. Použite Taylorov mnohočlen z predchádzajúceho cvičenia na
približný výpočet hodnoty ![]() . (Pomôcka: zvoľte
. (Pomôcka: zvoľte ![]() .)
.)
34. Dokážte, že rovnica
![]() má jediné
riešenie, ktoré patrí do intervalu
má jediné
riešenie, ktoré patrí do intervalu ![]() . Nahraďte funkciu na
ľavej strane rovnice jej Taylorovým mnohočlenom druhého stupňa a
zistite tak približnú hodnotu tohoto riešenia. Svoj výpočet
porovnajte s presným výpočtom.
. Nahraďte funkciu na
ľavej strane rovnice jej Taylorovým mnohočlenom druhého stupňa a
zistite tak približnú hodnotu tohoto riešenia. Svoj výpočet
porovnajte s presným výpočtom.
35. S chybou menšou ako ![]() vypočítajte hodnoty z
príkladu 26.
vypočítajte hodnoty z
príkladu 26.
36. Nájdite intervaly monotónnosti, intervaly, v ktorých je konvexná
a v ktorých konkávna a lokálne extrémy pre funkcie
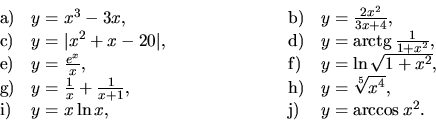
37. Dokážte, že postupnosť
![]() je
rastúca.
je
rastúca.
38. Nájdite najmenšiu a najväčšiu hodnotu funkcie v danom intervale
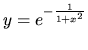 v intervale
v intervale
39. Aký najmenší obvod môže mať obdĺžnik s obsahom
![]() ?
?
40. Do rotačného kužeľa s polomerom ![]() a výškou
a výškou ![]() je vpísaný
valec tak, že jeho podstava leží v podstave kužeľa. Určte najväčšiu
možnú hodnotu
je vpísaný
valec tak, že jeho podstava leží v podstave kužeľa. Určte najväčšiu
možnú hodnotu
41. Pozemok v tvare obdĺžnika z jednej strany ohraničený rovným
prúdom rieky má byť zo zvyšných troch strán ohraničený plotom. Akú
môže mať pozemok najväčšiu plochu, ak môžeme na plot použiť ![]() metrov pletiva?
metrov pletiva?
42. Parník pohybujúci sa rovnomerne rýchlosťou ![]() km/h spotrebuje
za hodinu
km/h spotrebuje
za hodinu ![]()
![]() nafty. Pri akej
rýchlosti spotrebuje parník najmenej nafty?
nafty. Pri akej
rýchlosti spotrebuje parník najmenej nafty?
43. Z kartónu tvaru obdĺžnika ![]() cm má byť vyrobená
otvorená krabica tak, že sa v každom rohu vyreže štvorec a potom sa
zložia štyri bočné steny. Aký najväčší objem môže mať takto
vytvorená krabica?
cm má byť vyrobená
otvorená krabica tak, že sa v každom rohu vyreže štvorec a potom sa
zložia štyri bočné steny. Aký najväčší objem môže mať takto
vytvorená krabica?
44. Výrobca vynaloží na produkciu ![]() kusov výrobkov za týždeň
kusov výrobkov za týždeň
![]() Sk a je schopný ich predať za cenu
Sk a je schopný ich predať za cenu ![]() Sk za
kus.
Pri akom počte výrobkov za týždeň dosiahne výrobca najväčší zisk?
Koľko je tento zisk?
Sk za
kus.
Pri akom počte výrobkov za týždeň dosiahne výrobca najväčší zisk?
Koľko je tento zisk?
45. Chlapec stojí na jednom brehu rovnej rieky širokej ![]() km,
ktorá tečie rýchlosťou
km,
ktorá tečie rýchlosťou ![]() km/h a chce sa dostať na miesto na
opačnom brehu vzdialené
km/h a chce sa dostať na miesto na
opačnom brehu vzdialené ![]() km po prúde rieky. Za aký najmenší čas
to stihne, ak pláve rýchlosťou
km po prúde rieky. Za aký najmenší čas
to stihne, ak pláve rýchlosťou ![]() km/h a kráča rýchlosťou
km/h a kráča rýchlosťou ![]() km/h?
km/h?
46. Učiteľ dovolil študentom, aby si zvolili prirodzené číslo ![]() s
tým, že každý študent, ktorý bude mať z testu aspoň
s
tým, že každý študent, ktorý bude mať z testu aspoň
![]() bodov, urobí úspešne
skúšku. Aká hodnota
bodov, urobí úspešne
skúšku. Aká hodnota ![]() je pre študentov najvýhodnejšia?
je pre študentov najvýhodnejšia?
47. Nájdite príklad konvexnej funkcie ![]() , pre ktorú je funkcia
, pre ktorú je funkcia
![]() konkávna.
konkávna.
48.
49. Dokážte, že pre všetky
![]() platí
platí
![]() .
.
50. Dokážte, že pre všetky reálne čísla ![]() platí
platí
![]() .
.
51. Dokážte, že pre všetky
![]() platí
platí
![]() .
.
52. Dokážte, že pre všetky
![]() platí
platí
![]() .
.
53. Dokážte, že rovnica
![]() má jediné reálne
riešenie a nájdite interval dĺžky
má jediné reálne
riešenie a nájdite interval dĺžky ![]() , v ktorom sa toto
riešenie nachádza.
, v ktorom sa toto
riešenie nachádza.
54. Dokážte, že rovnica
![]() má jediné
kladné riešenie a nájdite interval dĺžky
má jediné
kladné riešenie a nájdite interval dĺžky ![]() , v ktorom sa toto
riešenie nachádza.
, v ktorom sa toto
riešenie nachádza.
55. Vyšetrite priebehy funkcií
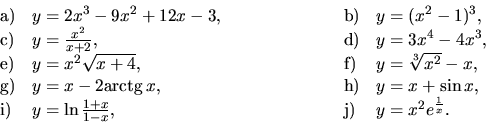
56.
Metódou bisekcie alebo metódou regula falsi určte aproximácie
koreňov rovníc
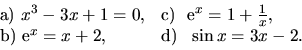
57.
Metódou bisekcie určte aproximácie
reálnych koreňov rovníc
![]() s presnosťou 0,01.
s presnosťou 0,01.
58.
Použijúc dva kroky metódy bisekcie, nájdite
približnú hodnotu reálneho koreňa rovnice
![]() , ktorý sa nachádza v intervale
, ktorý sa nachádza v intervale
![]() . Približné riešenia
. Približné riešenia
![]() vypočítajte na dve desatinné miesta.
Odhadnite chybu približnej hodnoty
vypočítajte na dve desatinné miesta.
Odhadnite chybu približnej hodnoty ![]() .
.
59.
Metódou regula falsi alebo metódou bisekcie určte
aproximáciu koreňov rovnice z predchádzajúceho
cvičenia s chybou
![]() . Pri metóde
bisekcie určte počet krokov potrebných k dosiahnutiu
požadovanej aproximácie.
. Pri metóde
bisekcie určte počet krokov potrebných k dosiahnutiu
požadovanej aproximácie.
60.
Metódou regula falsi nájdite aproximáciu kladného
koreňa rovnice
![]() s presnosťou
s presnosťou ![]() .
.
61.
Metódou prostej iterácie riešte rovnice z vyššie
uvedeného cvičenia. Preverte postačujúce podmienky
konvergencie. Iteračnýproces zastavte podmienkou
![]() . Určte odhad chyby
vypočítanej aproximácie koreňa.
. Určte odhad chyby
vypočítanej aproximácie koreňa.
62.
Metódou prostej iterácie riešte rovnicu
![]() . Posúďťe iteračné vzorce
. Posúďťe iteračné vzorce
63.
Nájdite aproximáciu najmenšieho nezáporného koreňa
nasledujúcich rovníc (s presnosťou ![]() ).
Použite metódu prostej iterácie.
).
Použite metódu prostej iterácie.
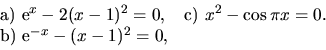
64.
Metódou prostej iterácie stanovte aproximáciu
dvoch najmenších kladných koreňov rovnice
![]() . Vyjasnite otázku konvergencie
metódy pre rôzne volené funkcie
. Vyjasnite otázku konvergencie
metódy pre rôzne volené funkcie ![]() .
.
65.
Nájdite aproximácie prvých dvoch kladných koreňov rovnice
![]() a) Newtonovou metódou b) metódou sečníc.
Výpočet zastavte, ak bude platiť
a) Newtonovou metódou b) metódou sečníc.
Výpočet zastavte, ak bude platiť
![]() .
Počiatočnú aproximáciu určte grafickou metódou.
.
Počiatočnú aproximáciu určte grafickou metódou.
66.
Použijúc dvakrát metódu dotyčníc,
nájdite približnú hodnotu reálneho koreňa
rovnice ![]() , ktorý sa nachádza v intervale
, ktorý sa nachádza v intervale
![]() . Približné hodnoty vypočítajte na dve
desatinné čísla. Odhadnite chybu približnej hodnoty
. Približné hodnoty vypočítajte na dve
desatinné čísla. Odhadnite chybu približnej hodnoty
![]() .
.
67.
Použijúc päťkrát metódu sečníc,
nájdite približné riešenie rovnice
![]() , ktoré sa nachádza v
intervale
, ktoré sa nachádza v
intervale
![]() s presnosťou na tri platné
číslice. Ako štartovaciu metódu použite
metódu delenia intervalu.
s presnosťou na tri platné
číslice. Ako štartovaciu metódu použite
metódu delenia intervalu.
68.
Vypočítajte približnú hodnotu koreňa
rovnice
![]() , ktorý
leží v intervale
, ktorý
leží v intervale
![]() .
Použite metódu sečníc s presnosťou na
päť desatinných miest.
.
Použite metódu sečníc s presnosťou na
päť desatinných miest.