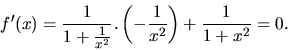AkDôsledkom je tvrdenie užitočné pri dôkazoch nerovností medzi funkciami.platí pre každé
, tak funkcia
je rastúca (klesajúca) v intervale
.
Nech funkcieIným dôsledkom vety o strednej hodnote je tvrdeniea
sú spojité v intervale
a
. Ak
pre každé
, tak aj
pre každé
.
Akpre všetky
, tak
je konštantná funkcia v intervale
.
Príklad 28.
Zistime intervaly, v ktorých rastú a intervaly, v ktorých
klesajú funkcie
![]() ,
,
![]() ,
, ![]() .
.
Riešenie:
Príklad 29.
Ukážeme, že pre každé ![]() platí
platí
![]() .
.
Riešenie: Nerovnosť ukážeme vtedy, ak sa presvedčíme, že
![]() pre každé
pre každé ![]() . Určíme intervaly, v
ktorých funkcia
. Určíme intervaly, v
ktorých funkcia ![]() rastie a v ktorých klesá.
rastie a v ktorých klesá. ![]() klesá v
klesá v
![]() a rastie v
a rastie v ![]() (overte!). Z toho vyplýva, že
funkcia
(overte!). Z toho vyplýva, že
funkcia ![]() nadobúda najmenšiu hodnotu v bode
nadobúda najmenšiu hodnotu v bode ![]() . Preto pre všetky
. Preto pre všetky
![]() platí
platí
![]() , čo sme chceli ukázať.
, čo sme chceli ukázať.
![]()
Príklad 30.
Ukážeme, že pre každé ![]() platí
platí
![]() .
.
Riešenie: Podobne ako v predchádzajúcom príklade uvažujme o funkcii
![]() . Chceme
ukázať, že
. Chceme
ukázať, že ![]() je konštantná a rovná
je konštantná a rovná ![]() v intervale
v intervale ![]() .
Jej derivácia je
.
Jej derivácia je