Ak je stav fyzikálnej veličiny v závislosti od času určený funkciou
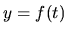 , tak rýchlosť zmeny tejto veličiny je určená
funkciou
, tak rýchlosť zmeny tejto veličiny je určená
funkciou 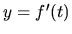 .
.
Preto, ak sa teleso pohybuje priamočiaro v
smere 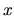 -ovej osi a jeho poloha v čase
-ovej osi a jeho poloha v čase 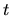 je
je 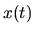 , tak funkcia
, tak funkcia
určuje jeho rýchlosť a funkcia
určuje jeho zrýchlenie v čase 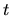 .
.
Príklad 19.
Do balóna guľového tvaru pripevneného spodným okrajom k zemi
prúdi rovnomerne 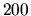 l vzduchu za minútu. Akou rýchlosťou sa
pohybuje smerom nahor vrchný okraj balóna v okamihu, keď sú v
balóne
l vzduchu za minútu. Akou rýchlosťou sa
pohybuje smerom nahor vrchný okraj balóna v okamihu, keď sú v
balóne 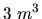 vzduchu?
vzduchu?
Riešenie: Označme 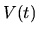 objem balóna v
objem balóna v 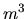 a
a 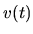 jeho výšku, teda
priemer v
jeho výšku, teda
priemer v 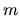 v čase
v čase 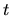 .
Potrebujeme zistiť veličinu
.
Potrebujeme zistiť veličinu 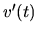 v čase, keď
v čase, keď 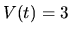 . Podľa
reťazového pravidla platí
. Podľa
reťazového pravidla platí
Veličina 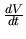 je rýchlosť prúdenia vzduchu a rovná sa
je rýchlosť prúdenia vzduchu a rovná sa
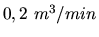 . Veličinu
. Veličinu 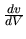 vyjadríme zo vzťahu pre
objem gule
vyjadríme zo vzťahu pre
objem gule
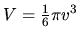 . Preto
. Preto
a
Dosadením dostávame hľadanú rýchlosť
čo je približne 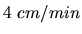 .
.

![]() l vzduchu za minútu. Akou rýchlosťou sa
pohybuje smerom nahor vrchný okraj balóna v okamihu, keď sú v
balóne
l vzduchu za minútu. Akou rýchlosťou sa
pohybuje smerom nahor vrchný okraj balóna v okamihu, keď sú v
balóne ![]() vzduchu?
vzduchu?
![]() objem balóna v
objem balóna v ![]() a
a ![]() jeho výšku, teda
priemer v
jeho výšku, teda
priemer v ![]() v čase
v čase ![]() .
Potrebujeme zistiť veličinu
.
Potrebujeme zistiť veličinu ![]() v čase, keď
v čase, keď ![]() . Podľa
reťazového pravidla platí
. Podľa
reťazového pravidla platí
![\begin{displaymath}
\frac{dv}{dV}_{[V = 3]} = \frac13 \sqrt[3]{\frac{6}{\pi 3^2}} =
\sqrt[3]{\frac{2}{81\pi}}.
\end{displaymath}](img2977.gif)