Existencia limity funkcie v bode vyjadruje istú ustálenosť hodnôt
funkcie v okolí tohoto bodu.
Voľne povedané, funkcia 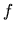 má v bode
má v bode  limitu
limitu 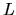 , ak
, ak
hodnoty funkcie 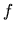 v číslach blízkych
v číslach blízkych  sú blízke
sú blízke 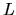 .
.
Pod bodom rozumieme ľubovoľné reálne číslo ako aj každú z
hodnôt 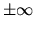 . Pod okolím bodu rozumieme ľubovoľný otvorený
interval obsahujúci tento bod.
. Pod okolím bodu rozumieme ľubovoľný otvorený
interval obsahujúci tento bod.
Funkcia 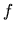 má v bode
má v bode  limitu
limitu 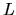 , ak sú splnené tieto podmienky:
, ak sú splnené tieto podmienky:
- Pre každé okolie
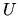 bodu
bodu  platí
platí
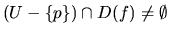
- pre každé okolie
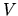 bodu
bodu 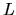 existuje také okolie
existuje také okolie 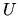 bodu
bodu  , že platí
, že platí
ak
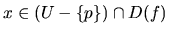 , tak
, tak 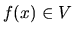 .
.
Fakt, že funkcia 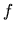 má v bode
má v bode  limitu
limitu 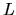 označujeme
označujeme
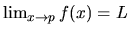 .
.
Ak bod  v predchádzajúcej definícii je reálne číslo, tak hovoríme
o limite vo vlastnom bode, v opačnom prípade hovoríme o
limite v nevlastnom bode. Ak hodnota
v predchádzajúcej definícii je reálne číslo, tak hovoríme
o limite vo vlastnom bode, v opačnom prípade hovoríme o
limite v nevlastnom bode. Ak hodnota 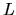 limity je reálne
číslo, tak hovoríme o vlastnej limite, v opačnom prípade
hovoríme o nevlastnej limite.
limity je reálne
číslo, tak hovoríme o vlastnej limite, v opačnom prípade
hovoríme o nevlastnej limite.
Ak má funkcia 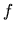 v bode
v bode  vlastnú limitu, hovoríme, že v bode
vlastnú limitu, hovoríme, že v bode  konverguje alebo je konvergentná, v opačnom
prípade v bode
konverguje alebo je konvergentná, v opačnom
prípade v bode  diverguje alebo je divergentná.
diverguje alebo je divergentná.
Funkcia 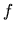 má v bode
má v bode  limitu
limitu 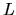 zľava (sprava) ,
ak má v bode
zľava (sprava) ,
ak má v bode  limitu
limitu 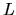 funkcia
funkcia
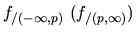 , označenie:
, označenie:
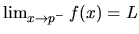 (
(
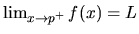 ).
Limity zľava a sprava nazývame spoločným názvom
jednostranné limity.
).
Limity zľava a sprava nazývame spoločným názvom
jednostranné limity.
Poznamenajme ešte, že ak má funkcia v niektorom bode limitu,
tak táto je určená jednoznačne.
v číslach blízkych
sú blízke
.
, tak
.