Pre prácu s nerovnosťami a nerovnicami platia tieto základné vlastnosti:
- Ak
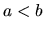 a
a 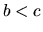 , potom
, potom 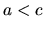 (tranzitívnosť).
(tranzitívnosť).
- Ak
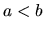 a
a 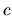 je ľubovoľné, potom
je ľubovoľné, potom 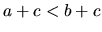 .
.
- Ak
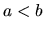 a
a 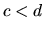 , potom
, potom 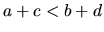 .
.
- Ak
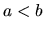 a
a 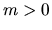 , potom
, potom 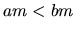 ; ak
; ak 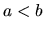 a
a 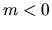 , potom
, potom 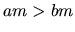 .
.
- Ak
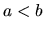 a
a 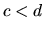 , kde
, kde 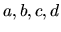 sú kladné
čísla, potom
sú kladné
čísla, potom 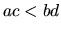 .
.
- Ak
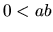 , potom je
, potom je 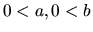 , alebo
, alebo 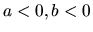 .
.
- Ak
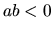 , potom je
, potom je 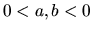 , alebo
, alebo 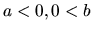 .
.
- Ak
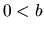 ,
, 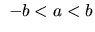 , potom je
, potom je 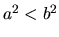 . Ak
. Ak
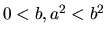 , je
, je 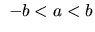 .
.
- Ak je
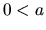 a
a 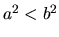 , potom platí:
alebo
, potom platí:
alebo 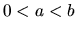 alebo
alebo 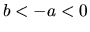 .
.
Tieto vlastnosti ostanú v platnosti aj keď znak 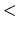 nahradíme znakom
nahradíme znakom
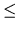 .
.
Lineárna nerovnica s jednou neznámou 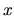 má tvar:
má tvar:
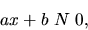 |
(1.3) |
kde 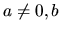 sú reálne čísla a
sú reálne čísla a
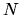 je niektorý zo znakov
je niektorý zo znakov
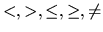 .
.
Kvadratická nerovnica s jednou neznámou je nerovnica tvaru:
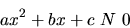 |
(1.4) |
kde 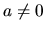 a
a 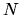 je opäť niektorý zo znakov
je opäť niektorý zo znakov
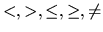 .
.
Riešením nerovnice (1.3) alebo (1.4) nazývame
množinu všetkých čísel, ktoré keď dosadíme do
nerovnice namiesto neznámej 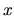 dostaneme pravdivú nerovnosť medzi číslami.
dostaneme pravdivú nerovnosť medzi číslami.
Systém lineárnych nerovníc s jednou neznámou má
tvar
kde
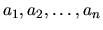 sú rôzne od nuly.
sú rôzne od nuly.
Nech riešenia jednotlivých nerovníc systému (1.5) sú
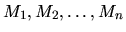 . Potom riešenie systému (1.5) je
. Potom riešenie systému (1.5) je
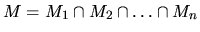 .
.
Ekvivalentnými nerovnicami nazývame také nerovnice, ktorých
množiny riešení sú rovnaké množiny. Úpravy, pomocou ktorých z
danej nerovnice dostaneme ekvivalentnú, nazývame ekvivalentnými
úpravami.
Pri riešení nerovníc používame vlastnosti 1.-9.
a to tak,
že z danej nerovnice dostávame ekvivalentné nerovnice, ktoré už vieme riešiť.
Kvadratickú nerovnicu (1.4) možno riešiť úpravou
na tvar
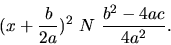 |
(1.6) |
Pri riešení tejto nerovnice môžu nastať tieto tri
prípady:
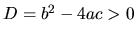 , nerovnicu (1.6) môžeme riešiť
napríklad úpravou na tvar
, nerovnicu (1.6) môžeme riešiť
napríklad úpravou na tvar
kde 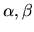 sú korene rovnice
sú korene rovnice 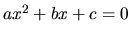 . Nerovnicu riešime ďalej podľa vlastností 5. a 6.
. Nerovnicu riešime ďalej podľa vlastností 5. a 6.
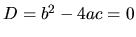 . Potom nerovnica (1.6) nemá riešenie, ak
. Potom nerovnica (1.6) nemá riešenie, ak
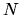 značí
značí 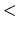 ; nerovnica (1.6) má riešenie
; nerovnica (1.6) má riešenie
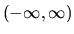 , ak
, ak 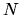 značí
značí 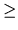 ; nerovnica (1.6) má riešenie
; nerovnica (1.6) má riešenie
 , ak
, ak 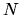 značí
značí 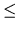 ; nerovnica
(1.6) má riešenie všetky reálne čísla okrem čísla
; nerovnica
(1.6) má riešenie všetky reálne čísla okrem čísla 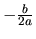 , ak
, ak 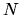 značí
značí 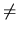 alebo
alebo 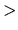 .
.
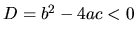 . Potom nerovnica (1.6)
nemá riešenie, ak
. Potom nerovnica (1.6)
nemá riešenie, ak 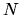 značí
značí 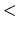 alebo
alebo 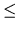 ; nerovnica (1.6) má riešenie
; nerovnica (1.6) má riešenie
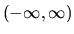 , ak
, ak 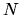 značí
značí 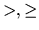 alebo
alebo 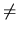 .
.
Príklad 15.
Riešme nerovnicu:
Riešenie:
Podľa vlastnosti 4. dostaneme po vynásobení oboch strán nerovnice
číslom 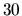 ekvivalentnú nerovnicu:
ekvivalentnú nerovnicu:
odkiaľ
K obom stranám nerovnice pripočítame výraz 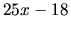 a podľa
vlastnosti 2. dostaneme
a podľa
vlastnosti 2. dostaneme
Vynásobením tejto nerovnice číslom 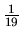 dostaneme
dostaneme
Riešením tejto nerovnice sú čísla z intervalu
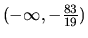 . Pri riešení sme robili len ekvivalentné úpravy, preto nájdené riešenie je aj riešením pôvodnej
nerovnice.
. Pri riešení sme robili len ekvivalentné úpravy, preto nájdené riešenie je aj riešením pôvodnej
nerovnice. 
Príklad 16.
Riešme nerovnicu:
Riešenie:
Pretože
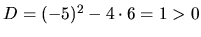 , danú nerovnicu riešime tak, že trojčlen
, danú nerovnicu riešime tak, že trojčlen 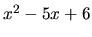 rozložíme na súčin koreňových činiteľov. Korene kvadratickej rovnice
rozložíme na súčin koreňových činiteľov. Korene kvadratickej rovnice 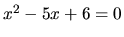 sú čísla
sú čísla 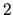 a
a 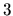 . Preto platí
. Preto platí
 . Dostávame
. Dostávame
Táto nerovnica je podľa vlastnosti 7. ekvivalentná s jedným z
nasledujúcich dvoch systémov
Riešením systému (1.7) je prienik
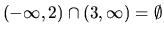 .
Riešením systému (1.8) je prienik
.
Riešením systému (1.8) je prienik
 . Riešením pôvodnej nerovnice
preto je
. Riešením pôvodnej nerovnice
preto je
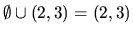 .
. 
Subsections
![]() ekvivalentnú nerovnicu:
ekvivalentnú nerovnicu:
![]() , danú nerovnicu riešime tak, že trojčlen
, danú nerovnicu riešime tak, že trojčlen ![]() rozložíme na súčin koreňových činiteľov. Korene kvadratickej rovnice
rozložíme na súčin koreňových činiteľov. Korene kvadratickej rovnice ![]() sú čísla
sú čísla ![]() a
a ![]() . Preto platí
. Preto platí
![]() . Dostávame
. Dostávame