Príklad 1.
Určte vlastné čísla matice
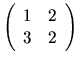 .
.
Riešenie:
Odpovedajúca homogénna sústava je tvaru
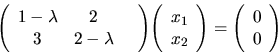
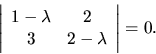
Podmienka
![]() sa pomocou
charakteristického polynómu matice A
sa pomocou
charakteristického polynómu matice A
Napriek tomu, že matica A má reálne koeficienty, môžu byť
niektoré jej vlastné čísla, keďže sú to korene
![]() , komplexnými
číslami.
, komplexnými
číslami.
Príklad 2.
Určte vlastné čísla matice
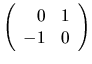 .
.
Riešenie:
Ľahko zistíme, že
![]() =
=
![]() , a preto vlastné čísla sú
, a preto vlastné čísla sú
![]() .
.
![]()
Ak
![]() (teda matica A je symetrická matica),
tak jej vlastné čísla sú reálne. Vlastné čísla diagonálnej matice a
trojuholníkovej matice sú rovné diagonálnym prvkom matice. Matica
A je regulárna práve vtedy, ak jej vlastné čísla sú rôzne od
nuly.
(teda matica A je symetrická matica),
tak jej vlastné čísla sú reálne. Vlastné čísla diagonálnej matice a
trojuholníkovej matice sú rovné diagonálnym prvkom matice. Matica
A je regulárna práve vtedy, ak jej vlastné čísla sú rôzne od
nuly.